题目内容
19．
实数a、b、c，如图，化简$\sqrt{{a}^{2}}$-|a-b|+$\sqrt{（b+c）^{2}}$．
分析 根据数轴上点的位置判断出绝对值里边式子的正负，利用绝对值的代数意义化简，合并即可得到结果．
解答 解：根据数轴上点的位置得：a＜-1＜c＜0＜1＜b，
∴a-b＜0，b+c＞0，
则原式=-a+a-b+b+c=c．
点评 此题考查了二次根式的性质与化简，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
实数a、b、c，如图，化简$\sqrt{{a}^{2}}$-|a-b|+$\sqrt{（b+c）^{2}}$．
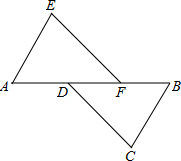如图，A、D、F、B在同一直线上，AD=BF，AE=BC，EF=DC，求证：CD∥EF．
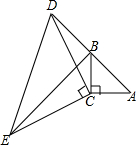如图，在△ABC中，∠ACB=90°，AC=BC，延长AB至点D，使DB=AB，连接CD，以CD为边作等腰直角三角形CDE，其中∠DCE=90°，连接BE．
如图是几个正方体所组成的几何体的俯视图，小正方形中的数字表示该位置小正方块的个数．请画出这个几何体的主视图和左视图．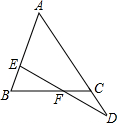
如图，已知△ABC中，AB=AC，D为AC延长线上一点，E为AB上一点，且BE=CD，连接DE交BC于点F，求证：DF=EF．