题目内容
关于x的方程kx2-
x+1=0有实数根,则k的取值范围是多少?
| 2k+1 |
考点:根的判别式,一元一次方程的解
专题:
分析:分类讨论:一元一次方程,一元二次方程,根据一元一次方程有实数根;一元二次方程要根据方程的判别式大于或等于零,方程有实数根,可得答案.
解答:解:当k≠0时,方程式一元二次方程,
由关于x的方程kx2-
x+1=0有实数根,得
△=(-
)2-4k=2k+1-4k≥0,
解得k≤
,即k≤0,或0≤k≤
;
当k=0时,方程是一元一次方程,方程有实数根,
综上所述:当k≤
时,关于x的方程kx2-
x+1=0有实数根.
由关于x的方程kx2-
| 2k+1 |
△=(-
| 2k+1 |
解得k≤
| 1 |
| 2 |
| 1 |
| 2 |
当k=0时,方程是一元一次方程,方程有实数根,
综上所述:当k≤
| 1 |
| 2 |
| 2k+1 |
点评:本题考查了根的判别式,分类讨论是解题关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
在下列立体图形中,侧面展开图是矩形的是( )
A、 |
B、 |
C、 |
D、 |
 如图,射线AB与AC所组成的角的表示方法不正确的是( )
如图,射线AB与AC所组成的角的表示方法不正确的是( )| A、∠1 | B、∠BAC |
| C、∠CAB | D、∠A |
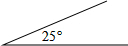 如图,某人沿着坡角为25°的斜坡走了500m,他上升的高度h为( )米.
如图,某人沿着坡角为25°的斜坡走了500m,他上升的高度h为( )米.| A、500sin25° | ||
| B、500cos25° | ||
| C、500tan25° | ||
D、
|
 如图,某城市A地和B地之间经常有车辆来往,H地和D地之间也经常有车辆来往,四地的坐标为:A(-3,2),D(1,1),H(-5,-3),B(-1,-4),拟建一座加油站,那么加油站建在哪里使它到A、B、D、H的距离之和最短,请在图中找到加油站的位置,并求出具体的位置坐标.
如图,某城市A地和B地之间经常有车辆来往,H地和D地之间也经常有车辆来往,四地的坐标为:A(-3,2),D(1,1),H(-5,-3),B(-1,-4),拟建一座加油站,那么加油站建在哪里使它到A、B、D、H的距离之和最短,请在图中找到加油站的位置,并求出具体的位置坐标.