题目内容
用不同的正多边形瓷砖进行地面铺设，若在一个顶点处有一个正三角形和一个正十边形，则还需一个正 边形瓷砖才能铺成平整无缝隙的地面．
考点：平面镶嵌（密铺）
专题：
分析：根据正三角形的每个内角为60°，正十边形的每个内角为144°，若能构成镶嵌，则还需正多边形的每个内角为360°-60°-144°=156°，据此即可求解．
解答：解：∵正三角形的每个内角为180°÷3=60°，
正十边形的每个内角为180°-
=144°，
∴还需正多边形的每个内角为360°-60°-144°=156°，
其每个外角为180°-156°=24°，
其边数为
=15．
故答案为：十五．
正十边形的每个内角为180°-
| 360° |
| 10 |
∴还需正多边形的每个内角为360°-60°-144°=156°，
其每个外角为180°-156°=24°，
其边数为
| 360 |
| 24 |
故答案为：十五．
点评：本题考查了平面镶嵌，欲解答此题，要熟悉平面镶嵌的定义还要熟悉正多边形内角和外角的求法．
练习册系列答案
相关题目
一副三角板有两个直角三角形，如图叠放在一起，那么∠α的度数是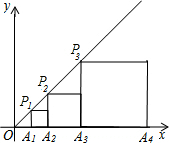
如图，直线l的解析式为y=x+1，点A1（1，0），过A1作x轴的垂线与直线l交于点P1．在线段A1P1右侧，以A1P1为边长作正方形，与x轴交于A2．过A2作x轴的垂线与直线l交于点P2．在线段A2P2右侧，以A2P2长为边长作正方形，与x轴交于A3．按照此法做下去，则P3的坐标为一次函数y=-2x+1的图象上有两点P（
，y1），Q（2，y2），则y1，y2的大小关系是（ ）
| 2 |
| A、y1＞y2 |
| B、y1＜y2 |
| C、y1=y2 |
| D、以上答案都有可能 |
下列图标中，既是中心对称又是轴对称的图案是（ ）
A、 |
B、 |
C、 |
D、 |