题目内容
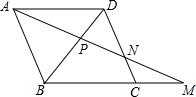已知：平行四边形ABCD中，过A作AM交BD于P，交CD于N，交BC的延长线于M，若PN=2，MN=6，则AP的长为
- A.3
- B.4
- C.
- D.8
B
分析：由平行四边形的性质：对边平行可得关于BP、PD、PM、PN、AP的比例式，进而得到问题答案．
解答：∵四边形ABCD是平行四边形，
∴AD∥BC，AB∥CD，
由AD∥BC得：
，
由AB∥CD得：
，
∴
，
∴AP2=PM•PN，
∵PN=2，MN=6，
∴PM=MN+PN=8，
∴AP2=16，
∴AP=4，
故选B．
点评：本题考查了平行四边形的对边平行的性质和平行线分线段成比例定理，解题的关键是挖掘出
为公共的比值．
分析：由平行四边形的性质：对边平行可得关于BP、PD、PM、PN、AP的比例式，进而得到问题答案．
解答：∵四边形ABCD是平行四边形，
∴AD∥BC，AB∥CD，
由AD∥BC得：
，由AB∥CD得：
，∴
，∴AP2=PM•PN，
∵PN=2，MN=6，
∴PM=MN+PN=8，
∴AP2=16，
∴AP=4，
故选B．
点评：本题考查了平行四边形的对边平行的性质和平行线分线段成比例定理，解题的关键是挖掘出
为公共的比值． 
练习册系列答案
相关题目
如图，已知在平行四边形ABCD中，点E在边BC上，射线AE交BD于点G，交DC的延长线于点F，AB=6，BE=3EC，求DF的长．已知在平行四边形ABCD中，向量
=
，
=
，那么向量
等于（ ）
| AB |
| a |
| BC |
| b |
| BD |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
于E，若BP=PD，
如图，已知在平行四边形ABCD中，点E、F分别在边AB、CD上，且AE=2EB，CF=2FD，连接EF．