题目内容
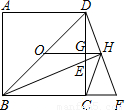
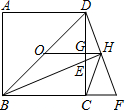
 如图所示,O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连接DF交BE的延长线于点H,连接OH交DC于点G,连接HC.则下列结论:①OH∥BF;②∠CHF=45°;③GH=
如图所示,O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连接DF交BE的延长线于点H,连接OH交DC于点G,连接HC.则下列结论:①OH∥BF;②∠CHF=45°;③GH= BC;④FH2=HE•HB,正确的是
BC;④FH2=HE•HB,正确的是
- A.①②③
- B.②③④
- C.①②④
- D.①③④
C
分析:根据正方形的性质及已知对各个结论进行分析,从而得到正确的个数.
解答: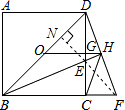 解:作EN⊥BD于N,连接EF.
解:作EN⊥BD于N,连接EF.
①∵BE平分∠DBC
∴EC=EN
∴等腰直角△DNE≌等腰直角△ECF,DE=FE
∴∠HEF=45°+22.5°=67.5°
∴∠HFE=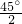 =22.5°
=22.5°
∴∠EHF=180°-67.5°-22.5°=90°
∵DH=HF
∴OH是△DBF的中位线
∴OH∥BF
②∠HCF=90°-22.5°=67.5°,∠HFC=45°+22.5°=67.5°,∠CHF=45°
③GH= CF=
CF= CE,CE<CG=
CE,CE<CG= BC,即CE<
BC,即CE< BC.
BC.
④△BHF∽△FHE,故FH2=HE•HB
所以①②④正确,故选C.
点评:解答此题的关键是作出两条辅助线,构造等腰直角三角形,利用等腰直角三角形的性质结合角平分线的性质逐步解答.
分析:根据正方形的性质及已知对各个结论进行分析,从而得到正确的个数.
解答:
 解:作EN⊥BD于N,连接EF.
解:作EN⊥BD于N,连接EF.①∵BE平分∠DBC
∴EC=EN
∴等腰直角△DNE≌等腰直角△ECF,DE=FE
∴∠HEF=45°+22.5°=67.5°
∴∠HFE=
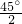 =22.5°
=22.5°∴∠EHF=180°-67.5°-22.5°=90°
∵DH=HF
∴OH是△DBF的中位线
∴OH∥BF
②∠HCF=90°-22.5°=67.5°,∠HFC=45°+22.5°=67.5°,∠CHF=45°
③GH=
 CF=
CF= CE,CE<CG=
CE,CE<CG= BC,即CE<
BC,即CE< BC.
BC.④△BHF∽△FHE,故FH2=HE•HB
所以①②④正确,故选C.
点评:解答此题的关键是作出两条辅助线,构造等腰直角三角形,利用等腰直角三角形的性质结合角平分线的性质逐步解答.

练习册系列答案
相关题目
 如图所示,O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连接DF交BE的延长线于点H,连接OH交DC于点G,连接HC.则下列结论:①OH∥BF;②∠CHF=45°;③GH=
如图所示,O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连接DF交BE的延长线于点H,连接OH交DC于点G,连接HC.则下列结论:①OH∥BF;②∠CHF=45°;③GH=| 1 |
| 4 |
| A、①②③ | B、②③④ |
| C、①②④ | D、①③④ |
 如图所示,P为正方形ABCD内一点,且PA:PB:PC=1:1:
如图所示,P为正方形ABCD内一点,且PA:PB:PC=1:1:| 3 |
| A、120 | B、135 |
| C、150 | D、175 |
 已知:如图所示,E为正方形ABCD外一点,AE=AD,∠ADE=75°,则∠AEB=
已知:如图所示,E为正方形ABCD外一点,AE=AD,∠ADE=75°,则∠AEB=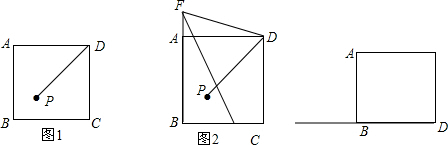
 BC;④FH2=HE•HB,正确的是( )
BC;④FH2=HE•HB,正确的是( )