题目内容
已知：如图所示，E为正方形ABCD外一点，AE=AD，∠ADE=75°，则∠AEB=30°
30°
．分析：根据等腰三角形的性质求出∠DAE，然后求出∠BAE的度数，再根据等腰三角形两底角相等列式计算即可得解．
解答：解：∵AE=AD，∠ADE=75°，
∴∠DAE=180°-2∠DAE=180°-2×75°=30°，
∴∠BAE=∠BAD+∠DAE=90°+30°=120°，
∵AB=AD，
∴AB=AE，
∴∠AEB=
（180°-∠BAE）=
×（180°-120°）=30°．
故答案为：30°．
∴∠DAE=180°-2∠DAE=180°-2×75°=30°，
∴∠BAE=∠BAD+∠DAE=90°+30°=120°，
∵AB=AD，
∴AB=AE，
∴∠AEB=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为：30°．
点评：本题考查了正方形的性质，等腰三角形两底角相等的性质，熟记性质并准确识图是解题的关键．
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
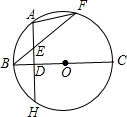A是弧BF的中点，AH⊥BC．
（2013•孝南区一模）已知，如图所示，AB为⊙O的直径，AB=AC，BC交⊙O于点D，AC交于⊙O于点E，∠BAC=45°，给出以下四个结论：
A是弧BF的中点，AH⊥BC．
已知：如图所示，△ABC为任意三角形，若将△ABC绕点C顺时针旋转180°得到△DEC．