题目内容
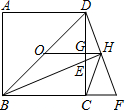
 如图所示,P为正方形ABCD内一点,且PA:PB:PC=1:1:
如图所示,P为正方形ABCD内一点,且PA:PB:PC=1:1:| 3 |
| A、120 | B、135 |
| C、150 | D、175 |
分析:将△APB绕B点逆时针旋转90°并连接PE,构造两个直角三角形:Rt△PBE和Rt△PEC,利用勾股定理逆定理解答即可.
解答: 解:将△APB绕B点逆时针旋转90°并连接PE,得△BEC,
解:将△APB绕B点逆时针旋转90°并连接PE,得△BEC,
∴△BEC≌△APB,∠APB=∠BEC,
∴△BEP为等腰直角三角形,
∴∠BEP=45°,
∵PB=1,
∴PE=
,
∵PC=
,CE=PA=1,
∴PC2=PE2+CE2,
∴∠PEC=90°,
∴∠APB=∠BEC=∠BEP+∠PEC=45°+90°=135°.
故选B.
 解:将△APB绕B点逆时针旋转90°并连接PE,得△BEC,
解:将△APB绕B点逆时针旋转90°并连接PE,得△BEC,∴△BEC≌△APB,∠APB=∠BEC,
∴△BEP为等腰直角三角形,
∴∠BEP=45°,
∵PB=1,
∴PE=
| 2 |
∵PC=
| 3 |
∴PC2=PE2+CE2,
∴∠PEC=90°,
∴∠APB=∠BEC=∠BEP+∠PEC=45°+90°=135°.
故选B.
点评:此题考查了旋转的性质及勾股定理逆定理,将将△APB绕B点顺时针旋转90°并连接PE是解题的关键.

练习册系列答案
相关题目
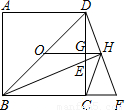
 如图所示,O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连接DF交BE的延长线于点H,连接OH交DC于点G,连接HC.则下列结论:①OH∥BF;②∠CHF=45°;③GH=
如图所示,O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连接DF交BE的延长线于点H,连接OH交DC于点G,连接HC.则下列结论:①OH∥BF;②∠CHF=45°;③GH= 已知:如图所示,E为正方形ABCD外一点,AE=AD,∠ADE=75°,则∠AEB=
已知:如图所示,E为正方形ABCD外一点,AE=AD,∠ADE=75°,则∠AEB=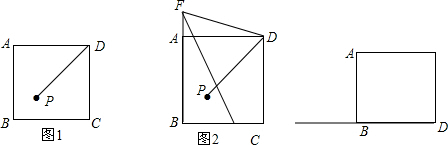
 BC;④FH2=HE•HB,正确的是( )
BC;④FH2=HE•HB,正确的是( )