题目内容
5.已知x1,x2,x3,x4的平均数是a,则3x1-5,3x2-8,3x3-6,3x4-1平均数是3a-5.分析 平均数的计算方法是求出所有数据的和,然后除以数据的总个数.先求数据x1,x2,x3,x4的和,然后再用平均数的定义求新数据的平均数.
解答 解:∵x1,x2,x3,x4的平均数是a,
∴$\frac{1}{4}$(x1+x2+x3+x4)=a,
∴x1+x2+x3+x4=4a,
∴另一组数据2x1-1,2x2-1,2x3-1,2x4-1的平均数是:
$\frac{1}{4}$(3x1-5+3x2-8+3x3-6+3x4-1)=$\frac{3}{4}$(x1+x2+x3+x4)-5=$\frac{3}{4}$×4a-5=3a-5.
故答案为3a-5.
点评 本题考查的是样本平均数的求法及运用,熟记算术平均数的计算公式是解决本题的关键.

练习册系列答案
相关题目
14.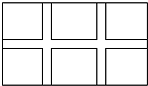 如图,学校课外生物小组的实验圆地是长35米、宽20米的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小道.要使种植面积为600平方米,若设小道的宽为x米,则所列方程正确的是( )
如图,学校课外生物小组的实验圆地是长35米、宽20米的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小道.要使种植面积为600平方米,若设小道的宽为x米,则所列方程正确的是( )
 如图,学校课外生物小组的实验圆地是长35米、宽20米的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小道.要使种植面积为600平方米,若设小道的宽为x米,则所列方程正确的是( )
如图,学校课外生物小组的实验圆地是长35米、宽20米的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小道.要使种植面积为600平方米,若设小道的宽为x米,则所列方程正确的是( )| A. | 35×20-2×20x-35x=600 | B. | 35×20-20x-35x+x2=600 | ||
| C. | (35-2x)(20-x)=600 | D. | (35-x)(20-x)=600 |
15.点A(-3,2)关于原点对称的点为点B,则点B的坐标是( )
| A. | (3,2) | B. | (-3,2) | C. | (3,-2) | D. | (-2,3) |
 如图所示的几何体是由四个小正方体组合而成的,请画出这个几何体从正面、左面和上面看到的图形.
如图所示的几何体是由四个小正方体组合而成的,请画出这个几何体从正面、左面和上面看到的图形.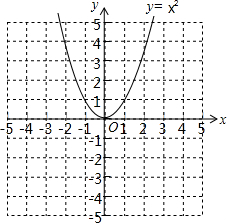 二次函数y=x2的图象如图,请将此图象向右平移1个单位,再向下平移4个单位.
二次函数y=x2的图象如图,请将此图象向右平移1个单位,再向下平移4个单位.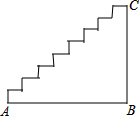 如图是小明家的楼梯示意图,其水平距离(即:AB的长度)为(2a+b)米,一只蚂蚁从A点沿着楼梯爬到C点,共爬了(3a-b)米.问小明家楼梯的竖直高点(即:BC的长度)为多少米.
如图是小明家的楼梯示意图,其水平距离(即:AB的长度)为(2a+b)米,一只蚂蚁从A点沿着楼梯爬到C点,共爬了(3a-b)米.问小明家楼梯的竖直高点(即:BC的长度)为多少米.