��Ŀ����
Ϊ�˹��������Լ��ˮ��ij�в��á�����ˮ�ۡ��ķ������¼���ÿ����ͥ��ˮ�ѣ�ÿ����ˮ��������20��ʱ����ÿ��2Ԫ�Ʒѣ�ÿ����ˮ������20��ʱ�����е�20����ÿ��2Ԫ�Ʒѣ��������ְ�ÿ��2.8Ԫ�Ʒѣ���ÿ����ͥÿ����ˮ��Ϊx��ʱ��Ӧ��ˮ��yԪ��
��1���ֱ����0��x��20��x��20ʱ��y��x֮��ĺ�������ʽ��
��2��Сӱ�����·ݡ����·ݷֱ�ˮ��45.6Ԫ��38Ԫ����Сӱ�����·ݱ����·ݽ�Լ��ˮ���ٶ֣�
�⣺��1����0��x��20ʱ��y��x�ĺ�������ʽ��y=2x��
��x��20ʱ��y��x�ĺ�������ʽ��y=2��20+2.8��x��20��=2.8x��16��
��2����ΪСӱ�����·ݵ�ˮ�Ѷ�������40Ԫ�����·ݵ�ˮ�ѳ���40Ԫ��
����y=38����y=2x����x=19��
��y=45.6����y=2.8x��16����x=22��
����22��19=3�֣�
��Сӱ�����·ݱ����·ݽ�Լ��ˮ3��

ij�̳������±ʴ����۵��������ͳ�����±���ʾ��
| ��ɫ | ��ɫ | ��ɫ | ��ɫ | ��ɫ | ��ɫ |
| ���������� | 56 | 128 | 520 | 210 | 16 |
�����������½��ʴ�ʱ���һЩ��ɫ�ģ���������һ����Ӧ�����ĸ�ͳ��֪ʶ��������
| �� | A�� | ƽ���� | B�� | ���� | C�� | ��λ�� | D�� | ���� |
��֪���κ���y=��x2+2bx+c����x��1ʱ��y��ֵ��xֵ���������С����ʵ��b��ȡֵ��Χ�ǣ�������
| �� | A�� | b�ݩ�1 | B�� | b�ܩ�1 | C�� | b��1 | D�� | b��1 |
Ҫʹʽ�� ��ʵ����Χ�������壬��x��ȡֵ��Χ�ǣ�������
��ʵ����Χ�������壬��x��ȡֵ��Χ�ǣ�������
| �� | A�� | x��1 | B�� | x��1 | C�� | x��1 | D�� | x��1 |
 0
0 ��
�� ���������Ľ⼯�������ϱ�ʾ������
���������Ľ⼯�������ϱ�ʾ������

 �߶�B0��0A�����˶�����A����0P�ij���y���˶�ʱ��t֮��ĺ���ͼ������ǣ�������
�߶�B0��0A�����˶�����A����0P�ij���y���˶�ʱ��t֮��ĺ���ͼ������ǣ�������




 ��ֱ�DZ�CD��y���ϣ��ҵ�C���A�غϣ�Rt��CDE��y��������ƽ���ƶ�������C�˶�����Oʱֹͣ�˶�������������⣺
��ֱ�DZ�CD��y���ϣ��ҵ�C���A�غϣ�Rt��CDE��y��������ƽ���ƶ�������C�˶�����Oʱֹͣ�˶�������������⣺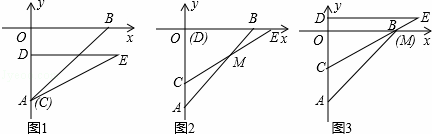
 ���������ǰ���
���������ǰ��� ����ƽ�Ƶ���ͼ��ʾ�����ߴ����Ƶ�
����ƽ�Ƶ���ͼ��ʾ�����ߴ����Ƶ� ��ʱ�뷽����ת
��ʱ�뷽����ת
 �������ǰ��б��������
�������ǰ��б�������� �ļн�
�ļн� Ϊ______
Ϊ______ .
.