题目内容
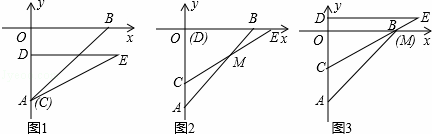
如图(1),在平面直角坐标系中,点A(0,﹣6),点B(6,0).Rt△CDE中,∠CDE=90°,CD=4,DE=4 ,直角边CD在y轴上,且点C与点A重合.Rt△CDE沿y轴正方向平行移动,当点C运动到点O时停止运动.解答下列问题:
,直角边CD在y轴上,且点C与点A重合.Rt△CDE沿y轴正方向平行移动,当点C运动到点O时停止运动.解答下列问题:
(1)如图(2),当Rt△CDE运动到点D与点O重合时,设CE交AB于点M,求∠BME的度数.
(2)如图(3),在Rt△CDE的运动过程中,当CE经过点B时,求BC的长.
(3)在Rt△CDE的运动过程中,设AC=h,△OAB与△CDE的重叠部分的面积为S,请写出S与h之间的函数关系式,并求出面积S的最大值.
解:(1)如图2,∵在平面直角坐标系中,点A(0,﹣6),点B(6,0).
∴OA=OB,
∴∠OAB=45°,
∵∠CDE=90°,CD=4,DE=4 ,
,
∴∠OCE=60°,
∴∠CMA=∠OCE﹣∠OAB=60°﹣45°=15°,
∴∠BME=∠CMA=15°;
(2)如图3,∵∠CDE=90°,CD=4,DE=4 ,
,
∴∠OBC=∠DEC=30°,
∵OB=6,
∴BC=4 ;
;
(3)①h≤2时,如图4,作MN⊥y轴交y轴于点N,作MF⊥DE交DE于点F,
∵CD=4,DE=4 ,AC=h,AN=NM,
,AC=h,AN=NM,
∴CN=4﹣FM,AN=MN=4+h﹣FM,
∵△CMN∽△CED,
∴ =
= ,
,
∴ =
= ,
,
解得FM=4﹣ ,
,
∴S=S△EDC﹣S△EFM= ×4×4
×4×4 ﹣
﹣ (4
(4 4﹣h)×(4﹣
4﹣h)×(4﹣ h)=﹣
h)=﹣ h2
h2 +4h+8,
+4h+8,
②如图3,当h≥2时,
S=S△OBC= OC×OB=
OC×OB= (6﹣h)×6=18﹣3h.
(6﹣h)×6=18﹣3h.




练习册系列答案
相关题目
在半径为2的圆中,弦AB的长为2,则 的长等于( )
的长等于( )
|
| A. |
| B. |
| C. |
| D. |
|
下列图形, 既是轴对称图形,又是中心对称图形的是( )
既是轴对称图形,又是中心对称图形的是( )
|
| A. |
| B. |
| C. |
| D. |
|












 综合成绩是由平时、期中和期末三项成绩按3:3:4的比例计算所得.若某同学本学期数学的平时、期中和期末成绩分别是90分,90分和85分,则他本学期数学学期综合成绩是 分.
综合成绩是由平时、期中和期末三项成绩按3:3:4的比例计算所得.若某同学本学期数学的平时、期中和期末成绩分别是90分,90分和85分,则他本学期数学学期综合成绩是 分.