题目内容
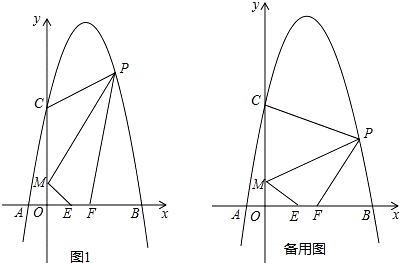
如图,对称轴为直线x=2的抛物线经过A(﹣1,0),C(0,5)两点,与x轴另一交点为B.已知M(0,1),E(a,0),F(a+1,0),点P是第 一象限内的抛物线上的动点.
一象限内的抛物线上的动点.
(1)求此抛物线的解析式;
(2)当a=1时,求四边形MEFP的面积的最大值,并求此时点P的坐标;
(3)若△PCM是以点P为顶点的等腰三角形,求a为何值时,四边形PMEF周长最小?请说明理由.
解:(1)∵对称轴为直线x=2,
∴设抛物线解析式为y=a(x﹣2)2+k.
将A(﹣1,0),C(0,5)代入得:
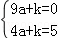 ,解得
,解得 ,
,
∴y=﹣(x﹣2)2+9=﹣x2+4x+5.
(2)当a=1时,E(1,0),F(2,0),OE=1,OF=2.
设P(x,﹣x2+4x+5),
如答图2,过点P作PN⊥y轴于点N,则PN=x,ON=﹣x2+4x+5,
∴MN=ON﹣OM=﹣x2+4x+4.
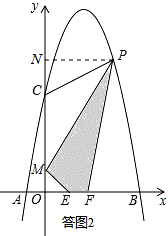
S四边形MEFP=S梯形OFPN﹣S△PMN﹣S△OME
=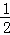 (PN+OF)•ON﹣
(PN+OF)•ON﹣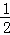 PN•MN﹣
PN•MN﹣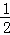 OM•OE
OM•OE
=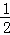 (x+2)(﹣x2+4x+5)﹣
(x+2)(﹣x2+4x+5)﹣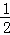 x•(﹣x2+4x+4)﹣
x•(﹣x2+4x+4)﹣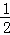 ×1×1
×1×1
=﹣x2+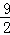 x+
x+
=﹣(x﹣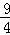 )2+
)2+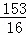
∴当x=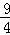 时,四边形MEFP的面积有最大值为
时,四边形MEFP的面积有最大值为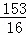 ,此时点P坐标为(
,此时点P坐标为(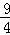 ,
,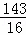 ).
).
(3)∵M(0,1),C(0,5),△PCM是以点P为顶点的等腰三角形,
∴点P的纵坐标为3.
令y=﹣x2+4x+5=3,解得x=2±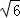 .
.
∵点P在第一象限,∴P(2+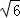 ,3).
,3).
四边形PMEF的四条边中,PM、EF长度固定,因此只要ME+PF最小,则PMEF的周长将取得最小值.
如答图3,将点M向右平移1个单位长度(EF的长度),得M1(1,1);
作点M1关于x轴的对称点M2,则M2(1,﹣1);
连接PM2,与x轴交于F点,此时ME+PF=PM2最小.

设直线PM2的解析式为y=mx+n,将P(2+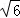 ,3),M2(1,﹣1)代入得:
,3),M2(1,﹣1)代入得:
 ,解得:m=
,解得:m=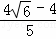 ,n=﹣
,n=﹣ ,
,
∴y= x﹣
x﹣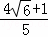 .
.
当y=0时,解得x=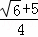 .∴F(
.∴F(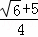 ,0).
,0).
∵a+1=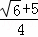 ,∴a=
,∴a= .
.
∴a= 时,四边形PMEF周长最小.
时,四边形PMEF周长最小.

 习题精选系列答案
习题精选系列答案研究发现人体在注射一定剂量的某种药后的数小时内,体内血液中的药物浓度(即血药浓度)y(毫克/升)是时间t(小时)的二次函数.已知某病人的三次化验结果如下表:
| t(小时) | 0 | 1 | 2 |
| y(毫克/升) | 0 | 0.14 | 0.24 |
(1)求y与t的函数解析式;
(2)在注射后的第几个小时,该病人体内的药物浓度达到最大?最大浓度是多少?
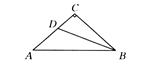
 ,cosB
,cosB .如果⊙O的半径为
.如果⊙O的半径为 cm,且经过点B、C,那么线段AO= cm.
cm,且经过点B、C,那么线段AO= cm.
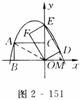
 和
和 都经过圆心O,则阴影部分的面积是 (结果保留π)
都经过圆心O,则阴影部分的面积是 (结果保留π)
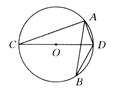
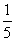 ,则AD的长为 ( )
,则AD的长为 ( )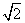 B.2 C.1 D.2
B.2 C.1 D.2