题目内容
如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.(1)求证:DE是⊙O的切线;
(2)若
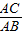 =
= ,求
,求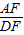 的值.
的值.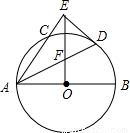
【答案】分析:(1)连接OD,只需证明OD⊥DE即可;
(2)连接BC,设AC=3k,AB=5k,BC=4k,可证OD垂直平分BC,利用勾股定理可得到OG,得到DG,于是AE=4k,然后通过OD∥AE,利用相似比即可求出 的值.
的值.
解答: (1)证明:连接OD,
(1)证明:连接OD,
∵OD=OA,
∴∠OAD=∠ADO,
∵∠EAD=∠BAD,
∴∠EAD=∠ADO,
∴OD∥AE,
∴∠AED+∠ODE=180°,
∵DE⊥AC,即∠AED=90°,
∴∠ODE=90°,
∴OD⊥DE,
∴DE是⊙O的切线;
 (2)解:连接BC,如图,
(2)解:连接BC,如图,
∵AB为直径,
∴∠ACB=90°,
又∵OD∥AE,
∴∠OGB=∠ACB=90°,
∴OD⊥BC,
∴G为BC的中点,即BG=CG,
又∵ =
= ,
,
∴设AC=3k,AB=5k,根据勾股定理得:BC= =4k,
=4k,
∴OB= AB=
AB= ,BG=
,BG= BC=2k,
BC=2k,
∴OG= =
= ,
,
∴DG=OD-OG= -
- =k,
=k,
又∵四边形CEDG为矩形,
∴CE=DG=k,
∴AE=AC+CE=3k+k=4k,
而OD∥AE,
∴ =
= =
= =
= .
.
点评:考查了切线的判定定理,能够综合运用角平分线的性质、全等三角形的判定和性质以及平行线分线段成比例定理.
(2)连接BC,设AC=3k,AB=5k,BC=4k,可证OD垂直平分BC,利用勾股定理可得到OG,得到DG,于是AE=4k,然后通过OD∥AE,利用相似比即可求出
 的值.
的值.解答:
 (1)证明:连接OD,
(1)证明:连接OD,∵OD=OA,
∴∠OAD=∠ADO,
∵∠EAD=∠BAD,
∴∠EAD=∠ADO,
∴OD∥AE,
∴∠AED+∠ODE=180°,
∵DE⊥AC,即∠AED=90°,
∴∠ODE=90°,
∴OD⊥DE,
∴DE是⊙O的切线;
 (2)解:连接BC,如图,
(2)解:连接BC,如图,∵AB为直径,
∴∠ACB=90°,
又∵OD∥AE,
∴∠OGB=∠ACB=90°,
∴OD⊥BC,
∴G为BC的中点,即BG=CG,
又∵
 =
= ,
,∴设AC=3k,AB=5k,根据勾股定理得:BC=
 =4k,
=4k,∴OB=
 AB=
AB= ,BG=
,BG= BC=2k,
BC=2k,∴OG=
 =
= ,
,∴DG=OD-OG=
 -
- =k,
=k,又∵四边形CEDG为矩形,
∴CE=DG=k,
∴AE=AC+CE=3k+k=4k,
而OD∥AE,
∴
 =
= =
= =
= .
.点评:考查了切线的判定定理,能够综合运用角平分线的性质、全等三角形的判定和性质以及平行线分线段成比例定理.

练习册系列答案
相关题目
 8、如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为( )
8、如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为( ) 0.1平方米)
0.1平方米)

 如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为
如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为