题目内容
18.点P(a+1,a-3)在第四象限,求a的取值范围.分析 根据第四象限的点的横坐标是正数,纵坐标是负数列出不等式组求解即可.
解答 解:∵点P(a+1,a-3)在第四象限,
∴$\left\{\begin{array}{l}{a+1>0}\\{a-3<}\end{array}\right.$,
解得-1<a<3.
点评 本题考查了各象限内点的坐标的符号特征以及解不等式,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
13.在平面直角坐标系中,点A到x轴的距离为1,到y轴的距离为2.若点A在第二象限,则A点坐标为( )
| A. | (-1,2) | B. | (2,-1) | C. | (-2,1) | D. | (2,1) |
3.下列各组数中,能构成直角三角形的一组是( )
| A. | 4,5,6 | B. | 3,3,3$\sqrt{2}$ | C. | 6,8,11 | D. | 5,12,14 |
10.直角坐标系中,点P(x,y)在第三象限,且P到x轴和y轴的距离分别为3、7,则点P的坐标为( )
| A. | (-3,-7) | B. | (-7,-3) | C. | (3,7) | D. | (7,3) |
 下图中有两个变量,你能将其中一个变量看做另一个变量的函数吗?
下图中有两个变量,你能将其中一个变量看做另一个变量的函数吗?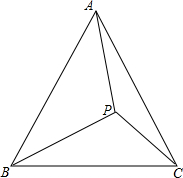 如图,在△ABC中,AB=BC,点P是△ABC内部的一点,∠BAP+∠BCP=90°,若AP=4,BP=5,CP=3,求证:△ABC为正三角形.
如图,在△ABC中,AB=BC,点P是△ABC内部的一点,∠BAP+∠BCP=90°,若AP=4,BP=5,CP=3,求证:△ABC为正三角形.