题目内容
如图所示,已知二次函数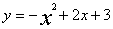 与坐标轴分别交于A、D、B三点,顶点为C。【原创】
与坐标轴分别交于A、D、B三点,顶点为C。【原创】
(1)求tan∠BAC
(2)在y轴上是否存在一点P,使得△DOP与△ABC相似,如果存在,求出点P的坐标,如果不存在,说明理由。
(3)Q是抛物线上一动点,使得以A、B、C、Q为端点的四边形是一个梯形,请直接写出满足条件的Q点的坐标。(不要求写出解题过程)
 |
解:(1)把y=0代入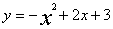 ,得
,得 。
。
解得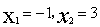
 即A(3,0),D(-1,0)
即A(3,0),D(-1,0)
把x=0代入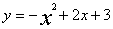 ,得y=3
,得y=3
∴B(0,3)
把x=1代入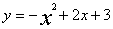
y=4,即C(1,4)。
过点C作CE⊥y轴,垂足为E。
∵△AOB和△BCE都是等腰直角三角形
∴∠ABC=90°且BC=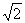 ,AB=
,AB= 。
。
∴tan∠BAC= 。。。。。4分
。。。。。4分
(2)①P在原点时,
∵PD=1,BP=3,∠BPD=∠ABC,且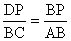
即△DOP∽△ABC。。。。。。。。。。。。。。。。2分
②当P在y轴负半轴时,设P(0,a)
由①知∠DBP=∠BAC。
∴只需∠BDP=Rt∠即可。
此时,易证△BDO∽△DOP
∴
∴OP=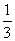
∴P(0,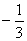 )。。。。。。。。。。。。。。。。2分
)。。。。。。。。。。。。。。。。2分
②当P在y轴正半轴时,显然△BDP不可能为Rt△。
∴所以满足题意的P点为(0,0)或(0,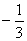 )。
)。
(3)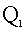 (-2,-5),
(-2,-5),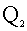 (4,-5),
(4,-5), (2,3)
(2,3)

练习册系列答案
相关题目
 xkb1.com
xkb1.com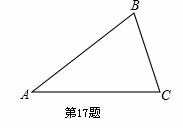 (2)作线段BD的垂直平分线交AB于点E,交BC于点F。由(1)(2)可得,你发现了BEDF是什么四边形?(原创)
(2)作线段BD的垂直平分线交AB于点E,交BC于点F。由(1)(2)可得,你发现了BEDF是什么四边形?(原创) ,则
,则 __________。
__________。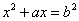 (a>0,b>0)的方程的图解法是:以
(a>0,b>0)的方程的图解法是:以 和b为两直角边做Rt△ABC,再在斜边上截取BD=
和b为两直角边做Rt△ABC,再在斜边上截取BD=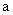 和线段b,作出方程的解。
和线段b,作出方程的解。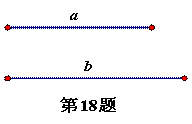
 ,则
,则 的取值范围是 .
的取值范围是 .  R C.
R C. R D.
R D. R
R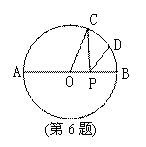
 )中的计算结果的规律填空:
)中的计算结果的规律填空: ,
, 的取值范围是 .
的取值范围是 . 
 .
.