题目内容

18．已知$\frac{x}{a-b}$=$\frac{y}{b-c}$=$\frac{z}{c-a}$，求$\frac{x+y+z}{2003a+2004b-2005c}$的值．

分析 令$\frac{x}{a-b}$=$\frac{y}{b-c}$=$\frac{z}{c-a}$=k，可得出x、y、z的值，求出x+y+z的值，代入代数式进行计算即可．

解答 解：∵令$\frac{x}{a-b}$=$\frac{y}{b-c}$=$\frac{z}{c-a}$=k，
∴x=（a-b）k，y=（b-c）k，z=（c-a）k，
∴x+y+z=（a-b）k+（b-c）k+（c-a）k=0，
∴$\frac{x+y+z}{2003a+2004b-2005c}$=0．

点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．

练习册系列答案
相关题目
10．已知多项式a3+$\frac{1}{2}$ab4-am+1b-6是六次四项式，单项式2x7-my3n与该多项式的次数相同．求：m2+n2的值．
9．对于方程x2=m-1，
（1）若方程有两个不相等的实数根，则m＞1；
（2）若方程有两个相等的实数根，则m=1；
（3）若方程无实数根，则m＜1．
6．探究：若数据x1，x2，x3，…xn的平均数是5，则：
数据x1+5，x2+5，x3+5，x4+5，…，xn+5的平均数是10；
数据x1-2，x2-2，x3-2，x4-2，x5-2的平均数是3；
数据2x1，2x2，2x3，2x4，2x5的平均数为10；
数据3x1-1，3x2-1，3x3-1，3x4-1，3x5-1的平均数是14．
由此我们可以猜想一个一般性的结论：若已知x1，x2，x3，…xn的平均数是$\overline{x}$，则：$\overline{x}$=$\frac{1}{n}$（x1+x2+…+xn）．
13．直角三角形的一直角边与斜边的比为12：13，而另一直角边长等于5cm，那么这个直角三角形的面积等于30cm2．
3．据统计，2014年某地区建筑商出售商品房后的利润率（利润除以成本）为25%．
（1）2014年该地区一套总售价为60万元的商品房，成本是多少？
（2）2015年第一季度，该地区商品房每平方米价格上涨了2a元，每平方米成本仅上涨了a元，这样60万元所能购买的商品房的面积比2014年减少了20平方米，建筑商的利润率上升了5个百分点，求2015年该地区建筑商出售的商品房每平方米的利润是多少？
10．我市是著名的苹果生产基地，果品公司从A村收购苹果400吨，每公斤10.2元，从B村收购苹果600吨，每公斤10.3元
（1）现在要将这些苹果就地卖给外地客商，若果品公司计划盈利10万元，则每公斤苹果多少钱？
（2）若将这些苹果运到C，D两个冷藏仓库储存，已知C仓库可储存300吨苹果，D仓库可储存700吨苹果，从A村运往C，D两处的费用分别为每吨20元和25元，从B村运往C，D两处的费用分别为每吨15元和18元．请你设计一个方案使苹果的运输费用最小，最小费用是多少？
（3）若按条件（2）将这些苹果储存到春节前出售，预计每公斤能卖到12元，但要损耗5%，那么春节前卖出这些苹果最多能盈利多少钱？
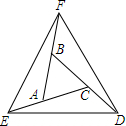7．如图，延长△ABC的各边，使得BF=AC，AE=CD=AB，顺次连接点D、E、F，得到△DEF为等边三角形．
（1）试说明△AEF≌△CDE；
（2）△ABC是等边三角形吗？请说明你的理由．
8．直接写出结果：
（1）（-9）+（+4）=-5   （2）（-9）-（+4）=-13．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网