题目内容
4.阅读:已知a+b=-4,ab=3,求a2+b2的值.解:∵a+b=-4,ab=3,
∴a2+b2=(a+b)2-2ab=(-4)2-2×3=10.
请你根据上述解题思路解答下面问题:
(1)已知a-b=-3,ab=-2,求(a+b)(a2-b2)的值.
(2)已知a-c-b=-10,(a-b)•c=-12,求(a-b)2+c2的值.
分析 (1)由于(a-b)2=(a+b)2-4ab,故采用整体代入法求解;
(2)根据完全平分公式,即可解答.
解答 解:(1)∵a-b=-3,ab=-2,
∴(a+b)(a2-b2)=(a+b)2(a-b)
=[(a-b)2+4ab](a-b)
=[(-3)2+4×(-2)]×(-3)
=-3.
(2)(a-b)2+c2=[(a-b)-c]2+2(a-b)c
=(-10)2+2×(-12)
=76.
点评 本题考查了完全平方公式,关键是要灵活应用完全平方公式及其变形公式.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
12.下列说法错误的是( )
| A. | 若两角互余,则两角均为锐角 | B. | 若两角相等,则它们的补角也相等 | ||
| C. | 互为余角的补角相等 | D. | 两个钝角不能互补 |
9.下列运算正确的是( )
| A. | a2•a3=a5 | B. | (x2)3=x5 | C. | m6÷m2=m3 | D. | 6a-4a=2 |
14.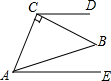 如图,CD∥AE,∠ACB=90°,AC=BC,∠BCD=20°,则∠EAB的度数为( )
如图,CD∥AE,∠ACB=90°,AC=BC,∠BCD=20°,则∠EAB的度数为( )
 如图,CD∥AE,∠ACB=90°,AC=BC,∠BCD=20°,则∠EAB的度数为( )
如图,CD∥AE,∠ACB=90°,AC=BC,∠BCD=20°,则∠EAB的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |




 如图,以点P为顶点,射线AB为一边,利用尺规作∠QPB,∠QPB=∠CAB.并说明PQ与AC的位置关系.
如图,以点P为顶点,射线AB为一边,利用尺规作∠QPB,∠QPB=∠CAB.并说明PQ与AC的位置关系.