题目内容
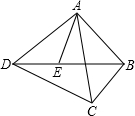 如图,点E是四边形ABCD的对角线BD上一点,且∠BAC=∠BDC=∠DAE.
如图,点E是四边形ABCD的对角线BD上一点,且∠BAC=∠BDC=∠DAE.(1)求证:△BEA∽△CDA;
(2)请猜想
| BC |
| DE |
考点:相似三角形的判定与性质
专题:
分析:(1)由三角形外角的性质及条件可得到∠AEB=∠ADC,结合条件可得到∠DAC=∠EAB,可证得结论;
(2)利用(1)的结论可证得△ADE∽△ACB,再利用相似三角形的性质可得出
=
或
(2)利用(1)的结论可证得△ADE∽△ACB,再利用相似三角形的性质可得出
| BC |
| DE |
| AB |
| AE |
| AC |
| AD |
解答:(1)证明:∵∠BAC=∠DAE,
∴∠DAE+∠EAC=∠BAC+∠EAC,
即∠BAE=∠DAC,
∵∠DAE=∠BDC,
∴∠DAE+∠ADE=∠BDC+∠ADE,
即∠AEB=∠ADC,
∴△BEA∽△CDA;
(2)解:
=
或
,证明如下:
由(1)可知△ADE∽△ACB,
∴
=
,且∠DAE=∠BAC,
∴△ADE∽△ACB,
∴
=
=
,
∴
=
或
.
∴∠DAE+∠EAC=∠BAC+∠EAC,
即∠BAE=∠DAC,
∵∠DAE=∠BDC,
∴∠DAE+∠ADE=∠BDC+∠ADE,
即∠AEB=∠ADC,
∴△BEA∽△CDA;
(2)解:
| BC |
| DE |
| AB |
| AE |
| AC |
| AD |
由(1)可知△ADE∽△ACB,
∴
| AB |
| AC |
| AE |
| AD |
∴△ADE∽△ACB,
∴
| BC |
| DE |
| AB |
| AE |
| AC |
| AD |
∴
| BC |
| DE |
| AB |
| AE |
| AC |
| AD |
点评:本题主要考查相似三角形的判定和性质,掌握相似三角形的判定方法是解题的关键,即①两个三角形的三边对应成比例、②两个三角形有两组角对应相等、③两个三角形的两组对边成比例且夹角相等,则这两个三角形相似.

练习册系列答案
相关题目
下列事件中的不可能事件是( )
| A、抛一枚硬币,落地后国徽一面朝下 |
| B、随意翻一下日历,翻到的号数是偶数 |
| C、这个月有雨 |
| D、今年夏天的最高气温达到了100℃ |
下列图中,∠1和∠2是对顶角的是( )
A、 |
B、 |
C、 |
D、 |

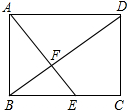 如图,四边形ABCD是矩形,点E在BC边上,AE与BD交于点F,∠BAE=∠ADB.
如图,四边形ABCD是矩形,点E在BC边上,AE与BD交于点F,∠BAE=∠ADB. 已知,在如图的数轴上有A、B、C三点,它们所表示的数依次是-1,+5和x.
已知,在如图的数轴上有A、B、C三点,它们所表示的数依次是-1,+5和x.