题目内容
20.一次函数y=2mx+3的图象与直线y=-x+1的交点在第二象限,则m的取值范围是m>-$\frac{1}{2}$.分析 首先联立方程组求得交点的坐标,再根据交点在第二象限列出不等式组,从而求得m的取值范围.
解答 解:根据题意,得-x+1=2mx+3,
解得x=-$\frac{2}{2m+1}$,
则y=$\frac{2m-1}{2m+1}$.
又交点在第二象限,则x<0,y>0,
即-$\frac{2}{2m+1}$<0,
解得m>-$\frac{1}{2}$.
故答案为:m>-$\frac{1}{2}$.
点评 考查了两条直线相交或平行问题,能够根据二元一次方程组求两条直线的交点,同时根据所在象限的位置确定字母的取值范围.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
11.根据下列表述,能确定位置的是( )
| A. | 东经118°,北纬40° | B. | 南京市白下路 | ||
| C. | 北偏东30° | D. | 红星电影院第2排 |
8.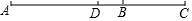 如图,已知线段AB=9,BC=5,点D为线段AC的中点,则线段AD的长度是( )
如图,已知线段AB=9,BC=5,点D为线段AC的中点,则线段AD的长度是( )
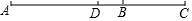 如图,已知线段AB=9,BC=5,点D为线段AC的中点,则线段AD的长度是( )
如图,已知线段AB=9,BC=5,点D为线段AC的中点,则线段AD的长度是( )| A. | 2 | B. | 2.5 | C. | 4.5 | D. | 7 |
11.为了从甲、乙两名学生中选择一人参加“文明城市创建”知识竞赛,在相同条件下对他们进行了10次测验,成绩如下:(单位:分)
(1)请完成下表:
(2)利用以上信息,请从三个不同的角度对甲、乙两名同学的成绩进行分析评价.
| 甲成绩 | 76 | 84 | 90 | 84 | 8l | 87 | 88 | 8l | 85 | 84 |
| 乙成绩 | 82 | 86 | 87 | 90 | 79 | 8l | 93 | 90 | 74 | 78 |
| 项目 学生 | 平均数 | 中位数 | 众数 | 方差 | 85分以上的频率 |
| 甲 | 84 | 84 | 84 | 14.4 | 0.3 |
| 乙 | 84 | 84 | 90 | 34 | 0.5 |
 (1)比较大小:$\sqrt{5}$+1>$\sqrt{10}$(填“>”、“<”或者“=”);
(1)比较大小:$\sqrt{5}$+1>$\sqrt{10}$(填“>”、“<”或者“=”); 如图,DE是△ABC的中位线,则△ADE与△ACB的面积的比是1:4.
如图,DE是△ABC的中位线,则△ADE与△ACB的面积的比是1:4.