题目内容
19. 如图,已知△ABC中,∠B是锐角,且∠B=2∠C,AD是BC边上的高.求证:AB+BD=DC.
如图,已知△ABC中,∠B是锐角,且∠B=2∠C,AD是BC边上的高.求证:AB+BD=DC.
分析 先在线段DC上取一点E,使DE=DB,连接AE,利用∠B=2∠C,求证△ACE是等腰三角形,然后利用等量代换即可求证结论.
解答 证明:在线段DC上取一点E,使DE=DB,连接AE,
∵AD⊥BC,
∴AD垂直平分BE,
∴AB=AE,
∴∠AEB=∠B,
∵∠B=2∠C,
∴∠AEB=2∠C,
∴∠EAC=∠AEB-∠C=2∠C-∠C=∠C,
∴AE=CE,
∴CE=AE=AB,
∴DC=DE+CE=AB+BD,
∴AB+BD=DC.
点评 此题主要考查学生对等腰三角形的判定与性质的理解和掌握,证明此题的关键是在线段DC上取一点E,使DE=DB,连接AE,这也是此题的突破点.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
4.两圆半径R、r分别是方程x2-3x+2=0的两根,且圆心距d=3,则两圆的位置关系是( )
| A. | 外离 | B. | 外切 | C. | 内含 | D. | 外离或内含 |
11.已知y=(k-2)x|k|-1+2k-3是关于x的一次函数,则k的值是( )
| A. | 2 | B. | -2 | C. | ±2 | D. | 0 |
8.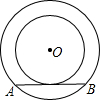 如图,以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线.若大圆半径为10cm,小圆半径为6cm,则弦AB的长为( )
如图,以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线.若大圆半径为10cm,小圆半径为6cm,则弦AB的长为( )
 如图,以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线.若大圆半径为10cm,小圆半径为6cm,则弦AB的长为( )
如图,以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线.若大圆半径为10cm,小圆半径为6cm,则弦AB的长为( )| A. | 8cm | B. | 10cm | C. | 12cm | D. | 16cm |
9.直线y=x-1的图象经过( )
| A. | 第二、三象限 | B. | 第一、二、四象限 | C. | 第一、三、四象限 | D. | 第一、二、三象限 |
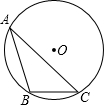 如图,△ABC内接于⊙O,∠A=30°,BC=4cm,求⊙O的直径是8cm.
如图,△ABC内接于⊙O,∠A=30°,BC=4cm,求⊙O的直径是8cm. 如图,正方形AOCB在平面直角坐标系xOy中,点O为原点,点B在反比例函数y=$\frac{k}{x}$(x>0)图象上,△BOC的面积为8.
如图,正方形AOCB在平面直角坐标系xOy中,点O为原点,点B在反比例函数y=$\frac{k}{x}$(x>0)图象上,△BOC的面积为8. 如图,
如图,