��Ŀ����
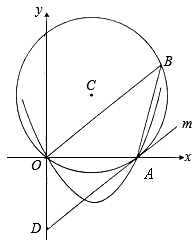
��ͼ����C���ڽӡ�AOB�У�AB=AO=4��tan��AOB= ��������y=ax2+bx������A(4��0)��㣨-2��6����
��������y=ax2+bx������A(4��0)��㣨-2��6����
��1���������ߵĺ�������ʽ��
��2��ֱ��m���C�����ڵ�A��y���ڵ�D������P���߶�OB�ϣ��ӵ�O�������B�˶���ͬʱ����Q���߶�DA�ϣ��ӵ�D�������A�˶�����P���ٶ�Ϊÿ��1����λ������Q���ٶ�Ϊÿ��2����λ������PQ��ADʱ�����˶�ʱ��t��ֵ��
��3����R��������λ��x���·����ֵ�ͼ���ϣ�����ROB������ʱ�����R������.
 ��������y=ax2+bx������A(4��0)��㣨-2��6����
��������y=ax2+bx������A(4��0)��㣨-2��6����
��1���������ߵĺ�������ʽ��
��2��ֱ��m���C�����ڵ�A��y���ڵ�D������P���߶�OB�ϣ��ӵ�O�������B�˶���ͬʱ����Q���߶�DA�ϣ��ӵ�D�������A�˶�����P���ٶ�Ϊÿ��1����λ������Q���ٶ�Ϊÿ��2����λ������PQ��ADʱ�����˶�ʱ��t��ֵ��
��3����R��������λ��x���·����ֵ�ͼ���ϣ�����ROB������ʱ�����R������.
��1��y= x2��2x����2��1.8����3����
x2��2x����2��1.8����3���� ��
��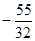 ��
��
 x2��2x����2��1.8����3����
x2��2x����2��1.8����3���� ��
��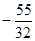 ��
�������������1����������y=ax2+bx������A��4��0����㣨-2��6�����ɸ��ݴ���ϵ������⣻
��2������O��OF��AD������AC��OB�ڵ�E���ɴ���������AC��OB���������ߵ����ʿɵ�AC��AD������֤���ı���OFAE�Ǿ��Σ���tan��AOB=
 �ɵ�sin��AOB=
�ɵ�sin��AOB=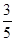 ���������AE��OD�ij�����PQ��ADʱ��OP=t��DQ=2t������Rt��ODF�У�OD=3��OF=AE=2.4��DF=DQ-FQ=DQ-OP=2t-t=t���ٸ��ݹ��ɶ�����⣻
���������AE��OD�ij�����PQ��ADʱ��OP=t��DQ=2t������Rt��ODF�У�OD=3��OF=AE=2.4��DF=DQ-FQ=DQ-OP=2t-t=t���ٸ��ݹ��ɶ�����⣻��3����ֱ��lƽ����OB��������������Ψһ����R�����У�����ʱ��ROB��OB���ϵĸ�������Դ�ʱ��ROB��������tan��AOB=
 �ɵ�ֱ��OB�Ľ���ʽΪy=
�ɵ�ֱ��OB�Ľ���ʽΪy= x����ֱ��lƽ����OB������ֱ��l����ʽΪy=
x����ֱ��lƽ����OB������ֱ��l����ʽΪy= x+b����R����ֱ��l�ϣ������������ϣ��ɵ�
x+b����R����ֱ��l�ϣ������������ϣ��ɵ� x2��2x=
x2��2x= x+b���ٸ���ֱ��l����������Ψһ����R�����У����ɵ÷���2x2-11x-4b=0��������ȵ�ʵ���������ɵõ��б�ʽ��=0���Ӷ�������ý����
x+b���ٸ���ֱ��l����������Ψһ����R�����У����ɵ÷���2x2-11x-4b=0��������ȵ�ʵ���������ɵõ��б�ʽ��=0���Ӷ�������ý������1����������y=ax2+bx������A��4��0����㣨-2��6����
��
 �����a=
�����a= ��b=��2
��b=��2�������ߵĽ���ʽΪ��y=
 x2��2x��
x2��2x����2������O��OF��AD������AC��OB�ڵ�E���ɴ���������AC��OB��

��ADΪ���ߣ�
��AC��AD��
��AD��OB��
���ı���OFAE�Ǿ��Σ�
��tan��AOB=

��sin��AOB=
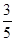 ��
����AE=OA��sin��AOB=4��
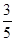 =2.4��
=2.4��OD=OA��tan��OAD=OA��tan��AOB=4��
 =3��
=3����PQ��ADʱ��OP=t��DQ=2t��
����Rt��ODF��OD=3��OF=AE=2.4��DF=DQ-FQ=DQ-OP=2t-t=t��
�ɹ��ɶ����ã�DF=
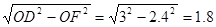 ��
����t=1.8�룻
��3����ֱ��lƽ����OB��������������Ψһ����R�����У���
��ʱ��ROB��OB���ϵĸ�������Դ�ʱ��ROB������
��tan��AOB=

��ֱ��OB�Ľ���ʽΪy=
 x��
x����ֱ��lƽ����OB������ֱ��l����ʽΪy=
 x+b��
x+b���ߵ�R����ֱ��l�ϣ������������ϣ�
��
 x2��2x=
x2��2x= x+b������ã�2x2-11x-4b=0��
x+b������ã�2x2-11x-4b=0����ֱ��l����������Ψһ����R�����У���
���2x2-11x-4b=0��������ȵ�ʵ����
���б�ʽ��=0����112+32b=0�����b=
 ��
����ʱԭ���̵Ľ�Ϊx=
 ����xR=
����xR=  ��
����yR=
 xR2��2xR=
xR2��2xR=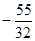
���R������ΪR��
 ��
��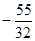 ����
�������������������dz�����ѧ���ص���ѵ㣬���п��м�Ϊ������һ����ѹ������ʽ���֣��ѶȽϴ�.

��ϰ��ϵ�д�
 �����Ƹ���ʦ����ϵ�д�
�����Ƹ���ʦ����ϵ�д� ��ͨ����ͬ����ϰ��ϵ�д�
��ͨ����ͬ����ϰ��ϵ�д�
�����Ŀ
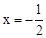
 ��
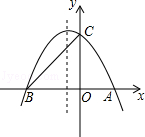
�� ����y�ύ�ڵ�A����Գ�����x�ύ�ڵ�B��
����y�ύ�ڵ�A����Գ�����x�ύ�ڵ�B��
 ��һ��λ��ֱ��l���Ϸ���������
��һ��λ��ֱ��l���Ϸ��������� ��һ��λ��ֱ��AB���·�����������ߵĽ���ʽ��
��һ��λ��ֱ��AB���·�����������ߵĽ���ʽ��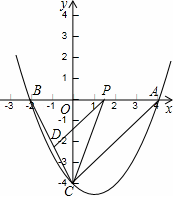
 ��
�� ���ڵ�
���ڵ� ����
���� ���ڵ�
���ڵ� ��������
�������� ����
���� ��1��0������.
��1��0������.
 ������Ϊ��-1��0������ֱ��
������Ϊ��-1��0������ֱ�� ��ʹ
��ʹ ��
�� ���ƣ������
���ƣ������ ��ʹ
��ʹ ����������ı���
����������ı��� �������������ڣ��������
�������������ڣ��������

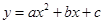 ��ͼ����
��ͼ����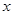 �ύ�ڣ��C 1��0������3��0��������˵����ȷ���ǣ� ��
�ύ�ڣ��C 1��0������3��0��������˵����ȷ���ǣ� ��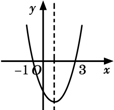

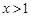 ʱ��y��xֵ�����������
ʱ��y��xֵ�����������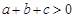
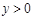 ʱ��
ʱ��