题目内容
在平面直角坐标系xOy中,抛物线 (
( )与y轴交于点A,其对称轴与x轴交于点B。
)与y轴交于点A,其对称轴与x轴交于点B。

(1)求点A,B的坐标;
(2)设直线l与直线AB关于该抛物线的对称轴对称,求直线l的解析式;
(3)若该抛物线在 这一段位于直线l的上方,并且在
这一段位于直线l的上方,并且在 这一段位于直线AB的下方,求该抛物线的解析式。
这一段位于直线AB的下方,求该抛物线的解析式。
 (
( )与y轴交于点A,其对称轴与x轴交于点B。
)与y轴交于点A,其对称轴与x轴交于点B。
(1)求点A,B的坐标;
(2)设直线l与直线AB关于该抛物线的对称轴对称,求直线l的解析式;
(3)若该抛物线在
 这一段位于直线l的上方,并且在
这一段位于直线l的上方,并且在 这一段位于直线AB的下方,求该抛物线的解析式。
这一段位于直线AB的下方,求该抛物线的解析式。(1) (2)
(2) (3)
(3)
 (2)
(2) (3)
(3)
解:(1)∵当 时,
时, 。∴A
。∴A 。
。
∵抛物线对称轴为 ,B
,B 。
。
(2)易得A点关于抛物线对称轴的对称点为 ,则直线l经过
,则直线l经过 、B,
、B,
设直线l的解析式为 ,
,
则 ,解得
,解得 。
。
∴直线l的解析式为 。
。
(3)∵抛物线对称轴为 。
。
∴抛物线在 这一段与在
这一段与在 这一段关于对称轴对称。
这一段关于对称轴对称。
结合图象可以观察到抛物线在 这一段位于直线l的上方在
这一段位于直线l的上方在 这一段位于直线l的下方,
这一段位于直线l的下方,
∴抛物线与直线l的交点横坐标为-1,代入直线l的解析式 得
得 。
。
∴抛物线过点(-1,4),代入抛物线的解析式得 ,解得
,解得 。
。
∴抛物线解析为 。
。
(1)令 即可求得A点坐标,根据公式求出抛物线对称轴即可求得B点坐标。
即可求得A点坐标,根据公式求出抛物线对称轴即可求得B点坐标。
(2)根据对称的性质求出A点关于抛物线对称轴对称的点的坐标,从而应用待定系数法即可求出直线l的解析式。
(3)由直线l与直线AB关于该抛物线的对称轴对称,和抛物线在 这一段位于直线l的上方,并且在
这一段位于直线l的上方,并且在 这一段位于直线AB的下方,得出抛物线在
这一段位于直线AB的下方,得出抛物线在 这一段位于直线l的上方在
这一段位于直线l的上方在 这一段位于直线l的下方,从而得出抛物线与直线l的交点横坐标为-1,进而先代入直线l的解析式求出交点纵坐标,再代入抛物线的解析式求出m,即可得到抛物线的解析式。
这一段位于直线l的下方,从而得出抛物线与直线l的交点横坐标为-1,进而先代入直线l的解析式求出交点纵坐标,再代入抛物线的解析式求出m,即可得到抛物线的解析式。
 时,
时, 。∴A
。∴A 。
。∵抛物线对称轴为
 ,B
,B 。
。(2)易得A点关于抛物线对称轴的对称点为
 ,则直线l经过
,则直线l经过 、B,
、B,设直线l的解析式为
 ,
,则
 ,解得
,解得 。
。∴直线l的解析式为
 。
。(3)∵抛物线对称轴为
 。
。∴抛物线在
 这一段与在
这一段与在 这一段关于对称轴对称。
这一段关于对称轴对称。结合图象可以观察到抛物线在
 这一段位于直线l的上方在
这一段位于直线l的上方在 这一段位于直线l的下方,
这一段位于直线l的下方,∴抛物线与直线l的交点横坐标为-1,代入直线l的解析式
 得
得 。
。∴抛物线过点(-1,4),代入抛物线的解析式得
 ,解得
,解得 。
。∴抛物线解析为
 。
。(1)令
 即可求得A点坐标,根据公式求出抛物线对称轴即可求得B点坐标。
即可求得A点坐标,根据公式求出抛物线对称轴即可求得B点坐标。(2)根据对称的性质求出A点关于抛物线对称轴对称的点的坐标,从而应用待定系数法即可求出直线l的解析式。
(3)由直线l与直线AB关于该抛物线的对称轴对称,和抛物线在
 这一段位于直线l的上方,并且在
这一段位于直线l的上方,并且在 这一段位于直线AB的下方,得出抛物线在
这一段位于直线AB的下方,得出抛物线在 这一段位于直线l的上方在
这一段位于直线l的上方在 这一段位于直线l的下方,从而得出抛物线与直线l的交点横坐标为-1,进而先代入直线l的解析式求出交点纵坐标,再代入抛物线的解析式求出m,即可得到抛物线的解析式。
这一段位于直线l的下方,从而得出抛物线与直线l的交点横坐标为-1,进而先代入直线l的解析式求出交点纵坐标,再代入抛物线的解析式求出m,即可得到抛物线的解析式。
练习册系列答案
相关题目
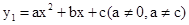 过点A(1,0),顶点为B,且抛物线不经过第三象限。
过点A(1,0),顶点为B,且抛物线不经过第三象限。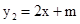 经过点B,且于该抛物线交于另一点C(
经过点B,且于该抛物线交于另一点C(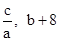 ),求当x≥1时y1的取值范围。
),求当x≥1时y1的取值范围。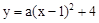 与x轴交于点A,B,与
与x轴交于点A,B,与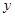 轴交于点C。过点C作CD∥x轴,交抛物线的对称轴于点D,连结BD。已知点A坐标为(-1,0)。
轴交于点C。过点C作CD∥x轴,交抛物线的对称轴于点D,连结BD。已知点A坐标为(-1,0)。
 ,抛物线y=ax2+bx经过点A(4,0)与点(-2,6).
,抛物线y=ax2+bx经过点A(4,0)与点(-2,6).
 于点B、C,则BC的长值为 .
于点B、C,则BC的长值为 .
 与x轴交于点A、B,与y轴交于点C,则△ABC的面积为 .
与x轴交于点A、B,与y轴交于点C,则△ABC的面积为 . 的开口向下,顶点坐标为(2,-3),那么该抛物线有( )
的开口向下,顶点坐标为(2,-3),那么该抛物线有( ) :
: 上的点,过点P的另一条直线
上的点,过点P的另一条直线 交抛物线
交抛物线 于A、B两点.
于A、B两点.
 ,求A、B两点的坐标;
,求A、B两点的坐标;  ),当PA=AB时,请直接写出点A的坐标;
),当PA=AB时,请直接写出点A的坐标; 轴于点C,若△AOB的外心在边AB上,且∠BPC=∠OCP,求点P的坐标.
轴于点C,若△AOB的外心在边AB上,且∠BPC=∠OCP,求点P的坐标. (克)与销售时间
(克)与销售时间 (月份)之间的函数图象. (4月份以30天计算)
(月份)之间的函数图象. (4月份以30天计算)