题目内容
已知：如图，在等腰梯形ABCD中，AD∥BC，∠BDC=∠BCD，点E是线段BD上一点，且BE=AD．
（1）证明：△ADB≌△EBC；
（2）直接写出图中所有的等腰三角形．
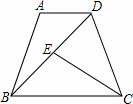
| 解（1）∵AD∥BC， ∴∠ADB=∠EBC， ∵∠BDC=∠BCD， ∴BD=BC， 在△ADB和△EBC中，
∴△ADB≌△EBC（SAS）．（2）由（1）可得△BCD是等腰三角形； ∵△ADB≌△EBC， ∴CE=AB， 又∵AB=CD， ∴CE=CD， ∴△CDE是等腰三角形． |
练习册系列答案
相关题目
下列计算正确的是（ ）
|
| A． |
| B． | （x+y）2=x2+y2 | C． | （﹣3x）3=﹣9x3 | D． | ﹣（x﹣6）=6﹣x |
CD．
如图，△ABC中，已知AB=8，∠C=90°，∠A=30°，DE是中位线，则DE的长为（ ）
|
| A． | 4 | B． | 3 | C． |
| D． | 2 |
为解的一个二元一次方
程是_________．