题目内容
已知二次函数y=-x2+4x+m的部分图象如图所示,则关于x的一元二次方程-x2+4x+m =0的解为 .

x1=-2,x2=6.
【解析】
试题分析:由二次函数y=-x2+4x+m的部分图象可以得到抛物线的对称轴和抛物线与x轴的一个交点坐标,然后可以求出另一个交点坐标,再利用抛物线与x轴交点的横坐标与相应的一元二次方程的根的关系即可得到关于x的一元二次方程-x2+4x+m=0的解.
试题解析:根据图示知,二次函数y=-x2+4x+m的对称轴为x=2,与x轴的一个交点为(6,0),
根据抛物线的对称性知,抛物线与x轴的另一个交点横坐标与点(6,0)关于对称轴对称,即x=-2,
则另一交点坐标为(-2,0)
则当x=-2或x=6时,函数值y=0,
即-x2+4x+m=0,
故关于x的一元二次方程-x2+4x+m=0的解为x1=-2,x2=6.
考点:抛物线与x轴的交点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 是一元二次方程,则m= ;
是一元二次方程,则m= ;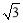 取1.732,结果精确到1米)
取1.732,结果精确到1米)

 的图象上,且k、x1、x2都是方程3-x=
的图象上,且k、x1、x2都是方程3-x= +9的根,则y1-y2的值为( )
+9的根,则y1-y2的值为( ) 的对称轴是( )
的对称轴是( ) B.直线
B.直线 C.y轴 D.直线x=2
C.y轴 D.直线x=2 .
.
 时,
时, 随
随 的
的