Question

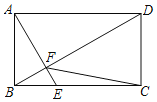
【题目】如图，已知是边长为的等边三角形，动点，同时从，两点出发，分别沿，匀速运动，其中点运动的速度是，点运动的速度是，当点到达点时，，两点都停止运动，设运动时间为，解答下列问题：

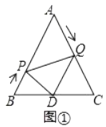
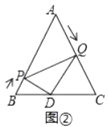
（1）如图①，当为何值时，；

（2）如图②，当为何值时，为直角三角形；

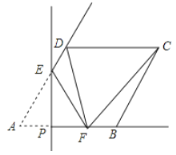
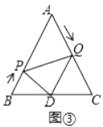
（3）如图③，作交于点，连接，当为何值时，与相似？

Answer 1

【答案】（1）；（2）3或；（3）或2

【解析】

（1）先表示出AQ=2t，AP=6-t，利用AP=3AQ建立方程求解即可得出结论；
（2）分两种情况，利用含30度角的直角三角形的性质（30度角所对的直角边是斜边的一半）建立方程求解即可得出结论；
（3）先表示出BD=2t，再分两种情况：①当△BPD∽△PDQ时，判断出∠APQ=∠BDP，进而判断出△APQ∽△BDP，得出比例式建立方程求解；
②当△BPQ∽△QDP时，得出∠B=∠DQP=60°，进而判断出△APQ是等边三角形，得出AP=AQ建立方程求解即可得出结论．

（1）由题意知，，，

∵是边长为的等边三角形，

∴，，

∴，

∵，

∴，

∴，

即：秒时，；

（2）由（1）知，，，

∵为直角三角形，

①当时，，

∴，∴秒，

②当时，，

∴，

∴秒，

即：秒或秒时，是直角三角形；

（3）由题意知，，，

∴，

∵是等边三角形，

∴，

∵，

∴，，

∴是等边三角形，

∴，

∴，

∵与相似，

∴①当时，

∴，

∴，

∵，

∴，

∴，

∴，

∴秒，

②当时，

∴，

∵，

∴，

∵，

∴是等边三角形，

∴，

∴，

∴秒，

即：秒或2秒时，与相似．