题目内容
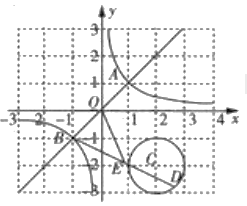
【题目】如图,反比例函数![]() 与正比例函数
与正比例函数![]() 交于格点(网格线的交点)
交于格点(网格线的交点)![]() .
.
(1)填空:![]() ;
;![]() ;
;
(2)当![]() 时,直接写出
时,直接写出![]() 时,
时,![]() 的取值范围;
的取值范围;
(3)点![]() 是以格点
是以格点![]() 为圆心,
为圆心, ![]() 为半径的圆上一动点,连接
为半径的圆上一动点,连接![]() 取
取![]() 的中点
的中点![]() 试确定线段
试确定线段![]() 的取值范围.
的取值范围.
【答案】(1)1,1;(2)![]() ;(3)线段
;(3)线段![]() 的取值范围为
的取值范围为![]()
【解析】
(1)根据题意可知反比例函数图象与正比例函数图象皆经过点A(1,1),由此将其坐标代入解析式求出![]() 的
的![]() 值即可;
值即可;
(2)先将![]() 变形为
变形为![]() ,然后根据函数图像进一步分析判断即可;
,然后根据函数图像进一步分析判断即可;
(3)如图所示,连接AD、AC,根据题意得出点![]() 是
是![]() 的中点,由此得知
的中点,由此得知![]() 是
是![]() 的中位线,故而
的中位线,故而![]() ,利用勾股定理求出
,利用勾股定理求出![]() ,最后结合题意,分情况讨论求出AD的最大值与最小值,从而进一步分析得出答案即可.
,最后结合题意,分情况讨论求出AD的最大值与最小值,从而进一步分析得出答案即可.
(1)∵反比例函数![]() 与正比例函数
与正比例函数![]() 皆经过点A(1,1),
皆经过点A(1,1),
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
故答案为:1,1;
(2)由![]() 可得
可得![]() ,
,
结合函数图象可知,此时![]() ,
,
∴当![]() 时,
时,![]() ;
;
(3)连接![]() 、AC,如图所示,
、AC,如图所示,

![]() 点
点![]() 的坐标为(1,1),点
的坐标为(1,1),点![]() 的坐标为
的坐标为![]() ,
,
![]() 点
点![]() 是
是![]() 的中点,
的中点,
又![]() 点
点![]() 是
是![]() 的中点,
的中点,
![]() 是
是![]() 的中位线,
的中位线,
![]() ,
,
又![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
![]() ,
,
![]() 点
点![]() 在以点
在以点![]() 为圆心,
为圆心,![]() 为半径的圆上,
为半径的圆上,
![]() ,
,
由题意可知:
当A、C、D三点共线,且点![]() 在线段
在线段![]() 上时,
上时,![]() 有最小值
有最小值![]() ,
,
当A、C、D三点共线,且点![]() 在
在![]() 的延长线上时,
的延长线上时,![]() 有最大值
有最大值![]() ,
,
![]() 的取值范围为
的取值范围为![]() ,
,
![]() 线段
线段![]() 的取值范围为
的取值范围为![]() .
.

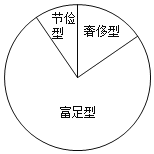
【题目】某校为了解学生零用钱支出情况,从七、八、九年级800名学生中随机抽取部分学生,对他们今年5月份的零用钱支出情况进行调查统计,并绘制成如下统计图表:
组别 | 零用钱支出x(单位:元) | 频数(人数) | 频率 | |
节俭型 | 一 | x<20 | m | 0.05 |
二 | 20≤x<30 | 4 | a | |
富足型 | 三 | 30≤x<40 | n | 0.45 |
四 | 40≤x<50 | 12 | b | |
奢侈型 | 五 | x≥50 | 4 | c |
合计 | 1 | |||
(1)表中a+b+c= ;m= ;本次调查共随机抽取了 名同学;
(2)在扇形统计图中,“富足型”对应的扇形的圆心角的度数是 ;
(3)估计今年5月份全校零花钱支出在30≤x<40范围内的学生人数;
(4)在抽样的“奢侈型”学生中,有2名女生和2名男生.学校团委计划从中随机抽取2名同学参加“绿苗理财计划”活动,请运用树状图或者列表说明恰好抽到一男一女的概率.