题目内容
5.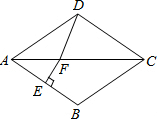 如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,E为垂足,连结DF,则∠CDF等于( )
如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,E为垂足,连结DF,则∠CDF等于( )| A. | 80° | B. | 70° | C. | 65° | D. | 60° |
分析 连接BF,根据菱形的对角线平分一组对角求出∠BAC,∠BCF=∠DCF,四条边都相等可得BC=DC,再根据菱形的邻角互补求出∠ABC,然后根据线段垂直平分线上的点到线段两端点的距离相等可得AF=BF,根据等边对等角求出∠ABF=∠BAC,从而求出∠CBF,再利用“边角边”证明△BCF和△DCF全等,根据全等三角形对应角相等可得∠CDF=∠CBF.
解答 解:如图,连接BF,
在菱形ABCD中,∠BAC=$\frac{1}{2}$∠BAD=$\frac{1}{2}$×80°=40°,∠BCF=∠DCF,BC=DC,
∠ABC=180°-∠BAD=180°-80°=100°,
∵EF是线段AB的垂直平分线,
∴AF=BF,∠ABF=∠BAC=40°,
∴∠CBF=∠ABC-∠ABF=100°-40°=60°,
∵在△BCF和△DCF中,$\left\{\begin{array}{l}{BC=DC}&{\;}\\{∠BCF=∠DCF}&{\;}\\{CF=CF}&{\;}\end{array}\right.$,
∴△BCF≌△DCF(SAS),
∴∠CDF=∠CBF=60°,
故选:D.
点评 本题考查了菱形的性质,全等三角形的判定与性质,线段垂直平分线上的点到线段两端点的距离相等的性质,综合性强,但难度不大,熟记各性质是解题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
15.如图所反映的两个量中,其中y是x的函数的个数有( )


| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
13.化简$\frac{{x}^{2}}{x-1}$-x+1的结果是( )
| A. | $\frac{1}{x-1}$ | B. | $\frac{1}{1-x}$ | C. | $\frac{1-2x}{x-1}$ | D. | $\frac{2x-1}{x-1}$ |
20.估算$\sqrt{30}$的值在( )
| A. | 3和4之间 | B. | 4和5之间 | C. | 5和6之间 | D. | 6和7之间 |
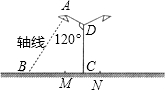 要在宽为36m的公路的绿化带MN(宽为4m)的中央安装路灯,路灯的灯臂AD的长为3m,且与灯柱CD成120°(如图所示),路灯采用圆锥形灯罩,灯罩的轴线AB与灯臂垂直.当灯罩的轴线通过公路路面一侧的中间时(除去绿化带的路面部分),照明效果最理想,问:应设计多高的灯柱,才能取得最理想的照明效果?(精确到0.01m,参考数据$\sqrt{3}$≈1.732)
要在宽为36m的公路的绿化带MN(宽为4m)的中央安装路灯,路灯的灯臂AD的长为3m,且与灯柱CD成120°(如图所示),路灯采用圆锥形灯罩,灯罩的轴线AB与灯臂垂直.当灯罩的轴线通过公路路面一侧的中间时(除去绿化带的路面部分),照明效果最理想,问:应设计多高的灯柱,才能取得最理想的照明效果?(精确到0.01m,参考数据$\sqrt{3}$≈1.732)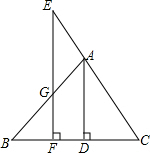 如图,已知AD⊥BC于点D,EF⊥BC于点F,交AB于点G,交CA的延长线于点E,∠E=∠AGE,求证:∠BAD=∠CAD.
如图,已知AD⊥BC于点D,EF⊥BC于点F,交AB于点G,交CA的延长线于点E,∠E=∠AGE,求证:∠BAD=∠CAD.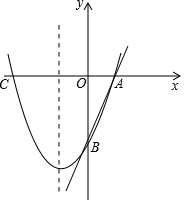 如图,已知直线y=3x-3分别交x轴、y轴于A、B两点,抛物线y=x2+bx+c经过
如图,已知直线y=3x-3分别交x轴、y轴于A、B两点,抛物线y=x2+bx+c经过