Question

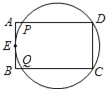
【题目】如图，平面直角坐标系中，一次函数（为常数，）的图像与轴、轴分别相交于点，半径为4的⊙与轴正半轴相交于点，与轴相交于点，点在点上方.

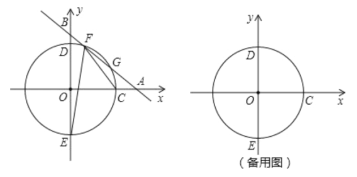
（1）若直线与弧有两个交点.

①求的度数；

②用含的代数式表示，并直接写出的取值范围；

（2）设，在线段上是否存在点，使？若存在，请求出点坐标；若不存在，请说明理由.

Answer 1

【答案】（1）①45°；②，（）；（2）b=5时存在，点P的坐标为，

当b>5时，直线与圆相离，不存在P，理由见解析.

【解析】

（1）连接CD，EA，利用同一条弦所对的圆周角相等求行∠CFE=45°，
（2）作OM⊥AB点M，连接OF，利用两条直线垂直相交求出交点M的坐标，利用勾股定理求出FM2，再求出FG2，再根据式子写出b的范围，
（3）当b=5时，直线与圆相切，存在点P，使∠CPE=45°，再利用△APO∽△AOB和△AMP∽△AOB相似得出点P的坐标，．

解：（1）①如图，

∵，

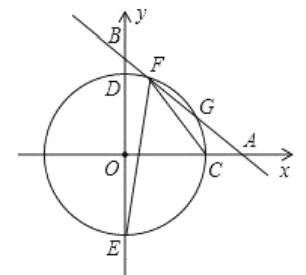
∴，（圆周角定理）

②方法一：

如图，作于，连接，

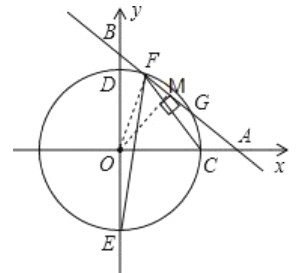
∵，直线的函数式为：，

∴所在的直线函数式为：，

∴交点

∴，

∵，

∴，

∵，

∴，

∵直线与弧有两个交点，

∴，

∴，（）

方法二：

如图，作于点，连接，

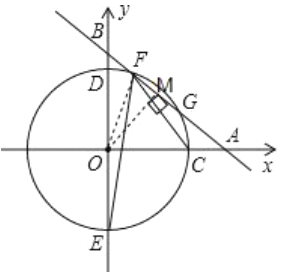
∵直线的函数式为：，

∴的坐标为，的坐标为，

∴，

∴，

∴，

∴，

∴在中，，

∵，

∴，

∵直线与弧有两个交点，

∴，

∴，（）

（2）如图，

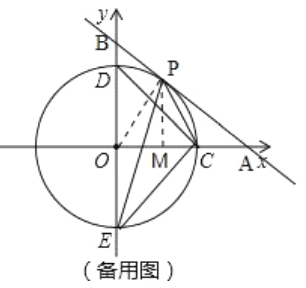
当时，直线与圆相切，

∵在直角坐标系中，，

∴，

∴存在点，使，

连接，

∵是切点，

∴，

∴∽，

∴，

∵，，，

∴，即，

∵，

作交于点，设的坐标为，

∵∽，

∴，

∴，

∴，

∴，

∴点的坐标为，

当时，直线与圆相离，不存在.

故答案为：（1）45°；（2），（）；（3）b=5时存在，点P的坐标为，

当b>5时，直线与圆相离，不存在P，理由见解析.