Question

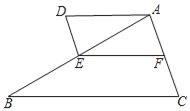
【题目】如图，已知点D在△ABC的外部，AD∥BC，点E在边AB上，ABAD＝BCAE．

（1）求证：∠BAC＝∠AED；

（2）在边AC取一点F，如果∠AFE＝∠D，求证：．

Answer 1

【答案】见解析

【解析】

（1）欲证明∠BAC＝∠AED，只要证明△CBA∽△DAE即可；

（2）由△DAE∽△CBA，可得，再证明四边形ADEF是平行四边形，推出DE＝AF，即可解决问题；

证明（1）∵AD∥BC，

∴∠B＝∠DAE，

∵AB·AD＝BC·AE，

∴，

∴△CBA∽△DAE，

∴∠BAC＝∠AED．

（2）由（1）得△DAE∽△CBA

∴∠D＝∠C，，

∵∠AFE＝∠D，

∴∠AFE＝∠C，

∴EF∥BC，

∵AD∥BC，

∴EF∥AD，

∵∠BAC＝∠AED，

∴DE∥AC，

∴四边形ADEF是平行四边形，

∴DE＝AF，

∴．