��Ŀ����
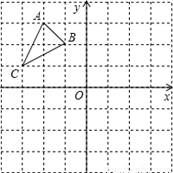
��֪A��2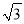 ��0����ֱ��y��(2��
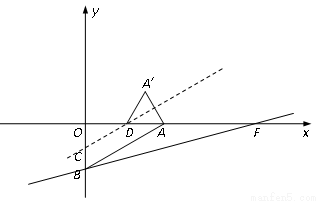
��0����ֱ��y��(2��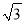 )x��2��x�ύ�ڵ�F����y�ύ�ڵ�B��ֱ��l��AB�ҽ�y���ڵ�C����x���ڵ�D����A����ֱ��l�ĶԳƵ�ΪA�䣬����AA�䡢A��D��ֱ��l��AB��������ÿ��1����λ���ٶ���y������������ƽ�ƣ����ƶ�ʱ��Ϊt��
)x��2��x�ύ�ڵ�F����y�ύ�ڵ�B��ֱ��l��AB�ҽ�y���ڵ�C����x���ڵ�D����A����ֱ��l�ĶԳƵ�ΪA�䣬����AA�䡢A��D��ֱ��l��AB��������ÿ��1����λ���ٶ���y������������ƽ�ƣ����ƶ�ʱ��Ϊt��
��1�����A�� �����꣨�ú�t�Ĵ���ʽ��ʾ����
��2����֤��AB��AF��
��3������C��ֱ��AB�Ĵ��߽�ֱ��y��(2��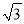 )x��2�ڵ�E���Ե�CΪԲ��CEΪ�뾶����C����tΪ��ֵʱ����C���AA��D��������ֱ�����У�
)x��2�ڵ�E���Ե�CΪԲ��CEΪ�뾶����C����tΪ��ֵʱ����C���AA��D��������ֱ�����У�
��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ


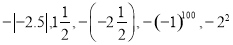 .
.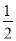 B. ֱ��x=-
B. ֱ��x=-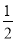 C. y�� D. ֱ��x��2
C. y�� D. ֱ��x��2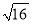 ������ƽ������4����
������ƽ������4����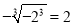 ���� a������ƽ������
���� a������ƽ������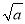 �����У���ȷ��˵���У�������
�����У���ȷ��˵���У�������