题目内容
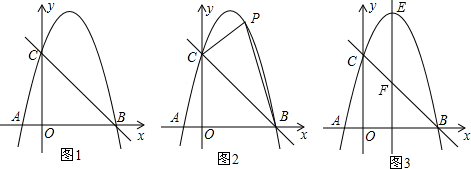
4.如图1,抛物线y=ax2+bx-4a经过A(-1,0)、C(0,4)两点,与x轴交于另一点B.(1)求抛物线的解析式;
(2)已知点D(m,m+1)在第一象限的抛物线上,求点D关于直线BC对称的点的坐标;
(3)如图2,点P为第一象限抛物线上一点,是否存在使△PBC面积最大的点P?若存在,求出点P的坐标;若不存在,请说明理由;
(4)如图3,若抛物线的对称轴EF(E为抛物线顶点)与直线BC相交于点F,M为直线BC上的任意一点,过点M作MN∥EF交抛物线于点N,以E,F,M,N为顶点的四边形能否为平行四边形?若能,求点N的坐标;若不能,请说明理由.
分析 (1)由于抛物线y=ax2+bx-4a经过A(-1,0)、C(0,4)两点,根据待定系数法可求抛物线的解析式;
(2)将点D(m,m+1)代入y=-x2+3x+4中,得到D(3,4),得到CD∥x轴,由B(4,0)、C(0,4)可得:OB=OC=4,根据等腰直角三角形的判定可得△OBC是等腰直角三角形,得:∠OCB=∠DCB=45°;再关于直线的对称点的性质即可求解;
(3)根据待定系数法可求直线BC的解析式,再根据三角形面积公式和二次函数的最值即可求解;
(4)根据抛物线y=-x2+3x+4的顶点坐标得到E$(\frac{3}{2},\frac{25}{4})$,直线BC:y=-x+4;当$x=\frac{3}{2}$时,y=-$\frac{3}{2}$+4=$\frac{5}{2}$,可得$F(\frac{3}{2},\frac{5}{2})$,根据两点间的距离公式可得$EF=\frac{15}{4}$,如图3,过点M作MN∥EF,交抛物线于点N,设N(x,-x2+3x+4),则M(x,-x+4);则MN=|(-x2+3x+4)-(-x+4)|=|-x2+4x|;当EF与NM平行且相等时,四边形EFMN是平行四边形,则|-x2+4x|=$\frac{15}{4}$,解方程可求点N的坐标.
解答 解:(1)依题意,有:$\left\{\begin{array}{l}{a-b-4a=0}\\{-4a=4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-1}\\{b=3}\end{array}\right.$.
故抛物线的解析式:y=-x2+3x+4.
(2)将点D(m,m+1)代入y=-x2+3x+4中,得:-m2+3m+4=m+1,
化简,得:m2-2m-3=0,
解得:m1=-1(舍),m2=3;
∴D(3,4),
∴CD∥x轴;
由B(4,0)、C(0,4)可得:OB=OC=4,即△OBC是等腰直角三角形,得:∠OCB=∠DCB=45°;
设点D关于直线BC的对称点为点E,则点E在y轴上,且CD=CE=3,OE=OC-CE=1,则:
点D关于直线BC的对称点的坐标为(0,1).
(3)由B(4,0)、C(0,4)可知,直线BC:y=-x+4;
如图2,过点P作PQ∥y轴,交直线BC于Q,设P(x,-x2+3x+4),则Q(x,-x+4);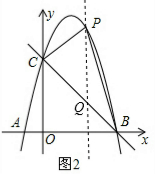 则PQ=(-x2+3x+4)-(-x+4)=-x2+4x;
则PQ=(-x2+3x+4)-(-x+4)=-x2+4x;
S△PCB=$\frac{1}{2}$PQ•OB=$\frac{1}{2}$×(-x2+4x)×4=-2(x-2)2+8;
所以,当P(2,6)时,△PCB的面积最大.
(4)存在.
抛物线y=-x2+3x+4的顶点坐标E$(\frac{3}{2},\frac{25}{4})$,
直线BC:y=-x+4;当$x=\frac{3}{2}$时,y=-$\frac{3}{2}$+4=$\frac{5}{2}$,
则$F(\frac{3}{2},\frac{5}{2})$,
则$EF=\frac{15}{4}$,
如图3,过点M作MN∥EF,交抛物线于点N,设N(x,-x2+3x+4),则M(x,-x+4);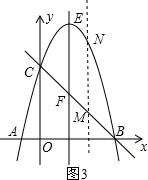 则MN=|(-x2+3x+4)-(-x+4)|=|-x2+4x|;
则MN=|(-x2+3x+4)-(-x+4)|=|-x2+4x|;
当EF与NM平行且相等时,四边形EFMN是平行四边形,
则|-x2+4x|=$\frac{15}{4}$
由$-{x^2}+4x=\frac{15}{4}$,解得${x_1}=\frac{5}{2},{x_2}=\frac{3}{2}$(不合题意,舍去),$当x=\frac{5}{2}时,y=-{(\frac{5}{2})^2}+3×\frac{5}{2}+4=\frac{21}{4}$,
则${N_1}(\frac{5}{2},\frac{21}{4})$,
由$-{x^2}+4x=-\frac{15}{4}$,解得${x_1}=2+\frac{1}{2}\sqrt{31},{x_2}=2-\frac{1}{2}\sqrt{31}$,
则N2($2+\frac{1}{2}\sqrt{31},-\frac{7}{4}-\frac{1}{2}\sqrt{31}$);N3(2-$\frac{1}{2}$$\sqrt{37}$,-$\frac{7}{4}$+$\frac{1}{2}$$\sqrt{37}$);
综上所述,存在平行四边形,点N的坐标为${N_1}(\frac{5}{2},\frac{21}{4})$,N2($2+\frac{1}{2}\sqrt{31},-\frac{7}{4}-\frac{1}{2}\sqrt{31}$);N3(2-$\frac{1}{2}$$\sqrt{37}$,-$\frac{7}{4}$+$\frac{1}{2}$$\sqrt{37}$).
点评 考查了二次函数综合题,解题的关键是熟练掌握待定系数法可求抛物线的解析式,等腰直角三角形的判定和性质,关于直线的对称点的性质,待定系数法求直线B解析式,三角形面积公式,二次函数的最值,抛物线的顶点坐标,两点间的距离公式,平行四边形的性质等知识点,以及方程思想,分类思想的应用,综合性较强,难度较大.

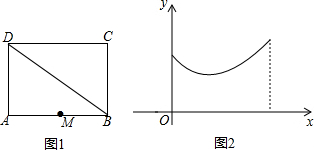 如图1,正方形ABCD中,点M是AB的中点,点P在某条线段上匀速运动,若运动的时间为x,点P与点M之间的距离为y,且表示y与x的函数关系的图象大致如图2所示,则点P的运动路线可能是( )
如图1,正方形ABCD中,点M是AB的中点,点P在某条线段上匀速运动,若运动的时间为x,点P与点M之间的距离为y,且表示y与x的函数关系的图象大致如图2所示,则点P的运动路线可能是( )| A. | A→B | B. | A→D | C. | B→D | D. | D→C |
| A. | 1个 | B. | 2个 | C. | 4个 | D. | 8个 |
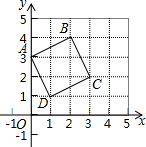 正方形ABCD在坐标系中的位置如图所示,将正方形ABCD沿x轴翻折一次,再沿轴翻折一次,然后向右平移1个单位记作:图形的一次完整变化,图形经历100次这样完整的变化后,点B到达的位置坐标为( )
正方形ABCD在坐标系中的位置如图所示,将正方形ABCD沿x轴翻折一次,再沿轴翻折一次,然后向右平移1个单位记作:图形的一次完整变化,图形经历100次这样完整的变化后,点B到达的位置坐标为( )| A. | (-1,-4) | B. | (2,4) | C. | (-1,-4) | D. | (1,4) |
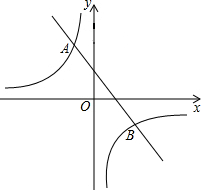 如图,一次函数的图象与反比例函数y=$\frac{{k}_{2}}{x}$(k2≠0)的图象交于A(-2,6)和点B(4,n)
如图,一次函数的图象与反比例函数y=$\frac{{k}_{2}}{x}$(k2≠0)的图象交于A(-2,6)和点B(4,n)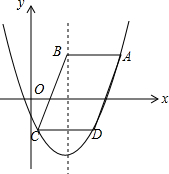 如图,在平面直角坐标系中,?ABCD的顶点A、C、D均在抛物线y=a(x-2)2+k(a>0)上,点B在抛物线的对称轴上,且AB∥x轴,若点A的横坐标为m,则点D的横坐标为$\frac{m+2}{2}$(用含m的代数式表示).
如图,在平面直角坐标系中,?ABCD的顶点A、C、D均在抛物线y=a(x-2)2+k(a>0)上,点B在抛物线的对称轴上,且AB∥x轴,若点A的横坐标为m,则点D的横坐标为$\frac{m+2}{2}$(用含m的代数式表示). 如图,数轴上A、B两点分别对应有理数a、b,则下列结论:①ab>0;②a-b>0;③a+b>0;④|a|-|b|>0中正确的有( )
如图,数轴上A、B两点分别对应有理数a、b,则下列结论:①ab>0;②a-b>0;③a+b>0;④|a|-|b|>0中正确的有( )