题目内容
19.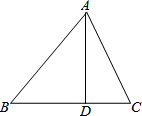 如图,在△ABC中,BD=6,AD=8,AB=10,DC=2,求AC的值.
如图,在△ABC中,BD=6,AD=8,AB=10,DC=2,求AC的值.
分析 首先根据勾股定理逆定理证明出△ADB是直角三角形,进而得到∠ADB=∠ADC=90°,再利用勾股定理计算出AC的长即可.
解答 解:在△ABD中,
∵BD2+AD2=62+82=102=AB2,
∴△ABD是直角三角形,∠ADB=90°,
∴∠ADC=90°.
在△Rt△ACD中,
AC2=DC2+AD2=22+82=68,
∴AC=$\sqrt{68}$=2$\sqrt{17}$.
点评 此题主要考查了勾股定理以及勾股定理的逆定理,用到的知识点:
勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.
勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
9.下列图形绕某点旋转180°后,不能与原来图形重合的是( )
| A. |  | B. |  | C. |  | D. |  |
14.下列各数中,无理数是( )
| A. | $\sqrt{7}$ | B. | 3 | C. | 0.101 | D. | -$\frac{2}{3}$ |