题目内容
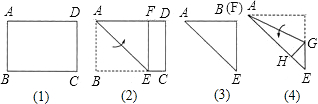
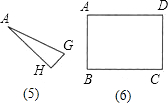
将矩形纸片ABCD沿过点B的直线折叠,使点A落在BC边上的点F处,折痕为BE(如图①);再沿过点E的直线折叠,使点D落在BE上的点D′处,折痕为EG(如图②);再展平纸片(如图③).则图③中∠α的大小为

- A.30°
- B.25.5°
- C.20°
- D.22.5°
D
分析:根据折叠不变性可知△AEB≌△FEB,求出∠AEB和∠FEB的度数为45°;再求出∠BED的度数,根据折叠不变性得∠BEG=∠DEG,进而计算出∠BEG的值,从而求出∠α的大小.
解答:由折叠不变性可知△AEB≌△FEB,
∴∠A=∠F=90°,
∵纸片ABCD是矩形,∴AE∥BF,
∴∠AEF=180°-∠F=90°,
∴∠AEB=∠FEB=45°,
∴∠BEG=∠DEG= =67.5°,
=67.5°,
∴∠α=67.5°-45°=22.5°.
故选D.
点评:此题结合矩形的性质考查了折叠不变性,找出图中的直角三角形、全等三角形是解题的关键.
分析:根据折叠不变性可知△AEB≌△FEB,求出∠AEB和∠FEB的度数为45°;再求出∠BED的度数,根据折叠不变性得∠BEG=∠DEG,进而计算出∠BEG的值,从而求出∠α的大小.
解答:由折叠不变性可知△AEB≌△FEB,
∴∠A=∠F=90°,
∵纸片ABCD是矩形,∴AE∥BF,
∴∠AEF=180°-∠F=90°,
∴∠AEB=∠FEB=45°,
∴∠BEG=∠DEG=
 =67.5°,
=67.5°,∴∠α=67.5°-45°=22.5°.
故选D.
点评:此题结合矩形的性质考查了折叠不变性,找出图中的直角三角形、全等三角形是解题的关键.

练习册系列答案
相关题目
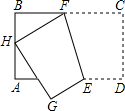 如图,将矩形纸片ABCD沿EF折叠,使得点C落在边AB上的点H处,点D落在点G处,若∠AHG=40°,则∠GEF的度数为( )
如图,将矩形纸片ABCD沿EF折叠,使得点C落在边AB上的点H处,点D落在点G处,若∠AHG=40°,则∠GEF的度数为( )| A、100° | B、110° | C、120° | D、135° |
 18、如图,将矩形纸片ABCD沿EF折叠后,点C、D分别落在点C′、D′处,若∠AFE=65°,则∠C′EF=
18、如图,将矩形纸片ABCD沿EF折叠后,点C、D分别落在点C′、D′处,若∠AFE=65°,则∠C′EF= 如图,将矩形纸片ABCD沿BD折叠,使点A落在点A′处,设A′B与CD相交于点E,若AB=8,BC=6,则EB=
如图,将矩形纸片ABCD沿BD折叠,使点A落在点A′处,设A′B与CD相交于点E,若AB=8,BC=6,则EB=