Question

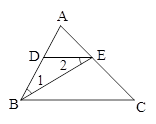
如图所示，BE是∠MBC的平分线，CE是∠NCB的平分线，连结AE。问：AE是∠MAN的平分线吗？为什么？

Answer 1

解：AE是∠MAN的平分线
理由：如图，作EH⊥AM于H，ED⊥BC于D，EP⊥AN于P

∵BE是∠MBC的平分线
∴EH=ED（角平分线上的点到角两边的距离相等）
同理，ED=EP
∴EH=EP
∴点E在∠MAN的平分线上（到角的两边距离相等的点，在这个角的平分线上）
∴AE平分∠MAN。