题目内容
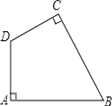
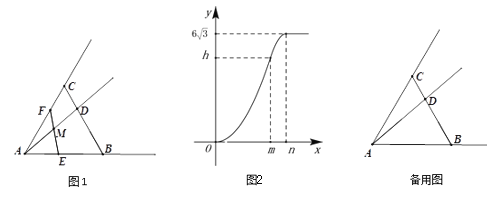
【题目】等腰直角
和等腰直角
分别在直线
上．
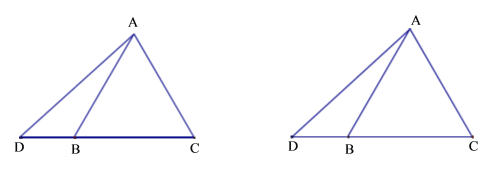
(1)如图所示，
分别在线段上，若
，求证：
．
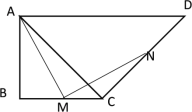
(2)若分别在线段外(还在直线上)，根据题意，画出图形，那么(1)的结论是否依然成立，若成立，写出证明过程；若不成立，说明原因；
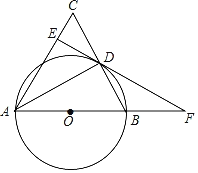
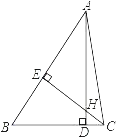
(3)如图，若，求证：．
【答案】（1）详见解析；（2）成立，详见解析；（3）详见解析
【解析】
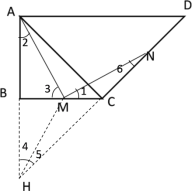
（1）延长
，交
的延长线于
，连接
，先证出△BHC为等腰直角三角形，然后证出BC是
的垂直平分线，根据垂直平分线的性质可得
，然后根据等边对等角和等角对等边证出HM=MN，即可证出结论；
（2）根据题意，分点M在CB的延长线和点M在BC的延长线两种情况讨论，分别画出对应的图形，根据垂直平分线的性质、等边对等角和等角对等边分别证明即可；
（3）延长，交的延长线于，连接，由(1)可得
是的垂直平分线，然后根据等边对等角和等量代换即可证出
，从而证出结论．
解：(1)延长，交的延长线于，连接．
，
，
又
，
，
∵等腰直角
和等腰直角
，
，
为等腰直角三角形，
，
又
，
，
是的垂直平分线，
，
，
，
而
，
，
(2)成立，证明如下
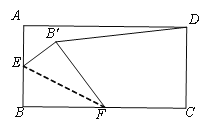
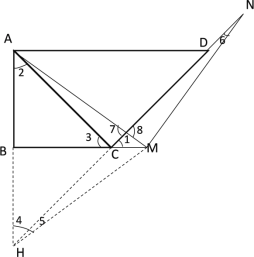
第一种情况：如图所示
延长
，交的延长线于，连接；
由(1)可得：
，
，
，
显然
是的垂直平分线，
，且
；
，
，
第二种情况：
易证显然
是的垂直平分线，
，
即
，
而
，∠7=∠8，
，
，
，
(3)延长，交的延长线于，连接．
由(1)可得是的垂直平分线，
，
∴
而
，
，
又
，
而，
，
，
．
练习册系列答案
相关题目
