Question

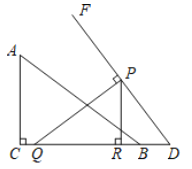
【题目】如图，在平面直角坐标中，点是坐标原点，一次函数与反比例函数的图象交于两点．

(1)求的值．

(2)根据图象写出当时，的取值范围．

(3)若一次函数图象与轴、轴分别交于点，则求出的面积．

Answer 1

【答案】（1）3；（2）；（3）6

【解析】

（1）将点A、B的坐标代入一次函数解析式中即可求出m和n，再将点B的坐标代入反比例函数解析式中即可求出k的值；

（2）根据点A、B的坐标和图象即可得出结论；

（3）连接OA，过点A作AD⊥x轴于D，先求出点N的坐标，从而求出ON，然后根据点A的坐标即可求出AD，最后根据三角形的面积公式计算即可．

解：(1)把两点的坐标代入，

得，

则．

把代入

得；

(2) ∵，

∴由函数图象可知，时，x的取值范围是；

(3)连接OA，过点A作AD⊥x轴于D

一次函数的图象与轴交于点，

∴即

∵，

∴AD=3

∴的面积=