题目内容

已知：CD为Rt△ABC的斜边上的高，且BC=a，AC=b，AB=c，CD=h（如图）．求证： $数学公式$ ．

证明：左边= $\text{[math]}$ = $\text{[math]}$
∵在直角三角形中，a²+b²=c²，
又∵ $\text{[math]}$ 即ab=ch
∴ $\text{[math]}$ =右边
即证得： $\text{[math]}$ ．
分析：将左边通分后用c²代替a²+b²，再根据等面积的不同表示形式可得出 $\text{[math]}$ 即ab=ch，将h代入右边可得出结论．
点评：本题考查勾股定理及三角形的面积，属于中等难度的试题，解答此类题目的方法就是两边凑，从而最终得出要证的结论．

练习册系列答案

朗朗阅读系列答案

同步练习册陕西科学技术出版社系列答案

应用题小状元应用题通关训练系列答案

考前小综合60练系列答案

考前专项分类高效检测系列答案

天天练口算系列答案

海东青跟踪测试系列答案

师说中考系列答案

中考酷题酷卷系列答案

初三中考总复习系列答案

相关题目

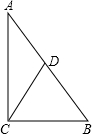
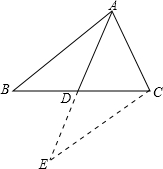阅读并解答问题．
如图，已知：AD为△ABC的中线，求证：AB+AC＞2AD．
证明：延长AD至E使得DE=AD，连接EC，则AE=2AD
∵AD为△ABC的中线
∴BD=CD
在△ABD和△CED中

，
∴△ABD≌△CED
∴AB=EC
在△ACE中，根据三角形的三边关系有
AC+EC

AE
而AB=EC，AE=2AD
∴AB+AC＞2AD
这种辅助线方法，我们称为“倍长中线法”，请利用这种方法解决以下问题：
（1）如图，已知：CD为Rt△ABC的中线，∠ACB=90°，求证：CD=

AB；
（2）把（1）中的结论用简洁的语言描述出来．

已知：CD为Rt△ABC的斜边上的高，且BC=a，AC=b，AB=c，CD=h（如图）．求证：

阅读并解答问题．
如图，已知：AD为△ABC的中线，求证：AB+AC＞2AD。
证明：延长AD至E使得DE=AD，连接EC，则AE=2AD
∵AD为△ABC的中线，
∴BD=CD
在△ABD和△CED中

，
∴△ABD≌△CED，
∴AB=EC，
在△ACE中，根据三角形的三边关系有AC+EC ____AE
而AB=EC，AE=2AD
∴AB+AC＞2AD
这种辅助线方法，我们称为“倍长中线法”，
请利用这种方法解决以下问题：
（1）如图，已知：CD为Rt△ABC的中线，∠ACB=90°，
求证：CD=

；
（2）把（1）中的结论用简洁的语言描述出来。

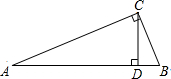已知：CD为Rt△ABC的斜边上的高，且BC=a，AC=b，AB=c，CD=h（如图）．求证：