Question

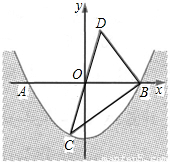某水渠的横截面呈抛物线，水面的宽度为AB（单位：米），现以AB所在直线为x轴，以抛物线的对称轴为y轴建立如图所示的平面直角坐标系，设坐标原点为O．已知AB=8米，设抛物线解析式为y=ax²-4．
（1）求a的值；
（2）点C（-1，m）是抛物线上一点，点C关于原点O的对称点为点D，连接CD，BC，BD，求△BCD的面积．

Answer 1

【答案】分析：（1）根据y轴为对称轴，AB=8，可得B（4，0），把B点坐标代入解析式即可求得a的值；
（2）根据（1）求得a的值，求出解析式，把C点坐标代入求得m的值，然后根据D、C关于原点对称求出D点坐标，然后根据S_△BCD=S_△BOD+S_△BOC求出面积即可．
解答：解：（1）∵AB=8，由抛物线的性质可知OB=4，
∴B（4，0），
把B点坐标代入解析式得：16a-4=0，
解得：a=；

（2）过点C作CE⊥AB于E，过点D作DF⊥AB于F，
∵a=，
∴y=x²-4，
令x=-1，
∴m=×（-1）²-4=-，
∴C（-1，-），
∵C关于原点对称点为D，
∴D的坐标为（1，），
则CE=DF=，
S_△BCD=S_△BOD+S_△BOC=OB•DF+OB•CE=×4×+×4×=15，
∴△BCD的面积为15平方米．
点评：本题考查了二次函数的应用，难度适中，解答本题的关键是熟练掌握用待定系数法函数解析式．