Question

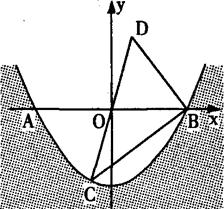
  某水渠的横截面呈抛物线形，水面的宽为AB(单位：米)。现以AB所在直线为x轴．以抛物线的对称轴为y轴建立如图所示的平面直角坐标系,设坐标原点为O．已知AB=8米。设抛物线解析式为y=ax²-4．

    (1)求a的值；

    (2)点C(一1，m)是抛物线上一点，点C关于原点0的对称点为点D，连接CD、BC、BD，求ABCD的面积．

Answer 1

考点：二次函数综合题。

分析：（1）首先得出B点的坐标，进而利用待定系数法求出a继而得二次函数解析式（2）首先得出C点的坐标，再由对称性得D点的坐标，由S_△BCD= S_△BOD+ S_△BOC求出

解答：(1)解∵AB=8  由抛物线的对称性可知0B=4

∴B(4，0)  0=16a-4∴a=

 (2)解：过点C作CE⊥AB于E，过点D作DF⊥AB于F

∵a=   ∴

令x=一1．∴m=×(一1)²—4=  ∴C(-1，)

∵点C关于原点对称点为D  ∴D(1，)．∴CE=DF=

S_△BCD= S_△BOD+ S_△BOC = =OB·DF+OB·CE=×4×+×4× =15

∴△BCD的面积为l5平方米