题目内容
 如图是二次函数y=ax2+bx+c图象的一部分.其对称轴为x=-1,且过点(-3,0).下列说法:
如图是二次函数y=ax2+bx+c图象的一部分.其对称轴为x=-1,且过点(-3,0).下列说法:(1)abc<0;(2)2a-b=0;(3)4a+2b+c=0;(4)若(-5,y1),(
| 5 |
| 2 |
其中说法正确的是
考点:二次函数图象与系数的关系
专题:
分析:根据图象分别求出a、b、c的符号,即可判断(1),根据对称轴求出b=2a,代入2a-b即可判断(2),把x=2代入二次函数的解析式,再根据二次函数的性质即可判断(3),求出点(-5,y1)关于直线x=-1的对称点的坐标,根据对称轴判断y1和y2的大小,即可判断(4).
解答:解:∵二次函数的图象开口向上,
∴a>0,
∵二次函数的图象交y轴的负半轴于一点,
∴c<0,
∵对称轴是直线x=-1,
∴-
=-1,
∴b=2a>0,
∴abc<0,
故(1)正确;
∵b=2a,
∴2a-b=0,
故(2)正确;
∵抛物线的对称轴为x=-1,且过点(-3,0),
∴抛物线与x轴另一交点为(1,0).
∵当x>-1时,y随x的增大而增大,
∴当x=2时y>0,即4a+2b+c>0,
故(3)错误;
∵(-5,y1)关于直线x=-1的对称点的坐标是(3,y1),
又∵当x>-1时,y随x的增大而增大,3>
,
∴y1>y2,
故(4)正确;
故答案为(1)(2)(4).
∴a>0,
∵二次函数的图象交y轴的负半轴于一点,
∴c<0,
∵对称轴是直线x=-1,
∴-
| b |
| 2a |
∴b=2a>0,
∴abc<0,
故(1)正确;
∵b=2a,
∴2a-b=0,
故(2)正确;
∵抛物线的对称轴为x=-1,且过点(-3,0),
∴抛物线与x轴另一交点为(1,0).
∵当x>-1时,y随x的增大而增大,
∴当x=2时y>0,即4a+2b+c>0,
故(3)错误;
∵(-5,y1)关于直线x=-1的对称点的坐标是(3,y1),
又∵当x>-1时,y随x的增大而增大,3>
| 5 |
| 2 |
∴y1>y2,
故(4)正确;
故答案为(1)(2)(4).
点评:本题考查了二次函数图象与系数的关系:二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小,当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左侧; 当a与b异号时(即ab<0),对称轴在y轴右侧.(简称:左同右异).抛物线与y轴交于(0,c).抛物线与x轴交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
为迎接“五一”的到来,同学们做了许多拉花布置教室准备召开“五一”联欢晚会,小刚搬来一架高2.5米的木梯,准备把拉花挂到2.4米高的墙上,则梯脚与墙距离应为( )
| A、0.7米 | B、0.8米 |
| C、0.9米 | D、1.0米 |
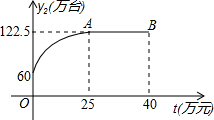 某公司开发了一种新型的家电产品,又适逢“家电下乡”的优惠政策.现投资40万元用于该产品的广告促销,已知该产品的本地销售量y1(万台)与本地的广告费用x(万元)之间的函数关系满足y1=3x+25,该产品的外地销售量y2(万台)与外地广告费用t(万元)之间的函数关系可用如图所示的抛物线和线段AB来表示.其中点A为抛物线的顶点.
某公司开发了一种新型的家电产品,又适逢“家电下乡”的优惠政策.现投资40万元用于该产品的广告促销,已知该产品的本地销售量y1(万台)与本地的广告费用x(万元)之间的函数关系满足y1=3x+25,该产品的外地销售量y2(万台)与外地广告费用t(万元)之间的函数关系可用如图所示的抛物线和线段AB来表示.其中点A为抛物线的顶点. 如图,在四边形ABCD中,∠B=90°,∠BCD=135°,且AB=3cm,BC=7cm,CD=5
如图,在四边形ABCD中,∠B=90°,∠BCD=135°,且AB=3cm,BC=7cm,CD=5