题目内容
9.直线y1=k1x+b1与直线y2=k2x+b2交y轴于同一点,则b1和b2的关系是( )| A. | b1>b2 | B. | b1<b2 | C. | b1=b2 | D. | 不能确定 |
分析 根据一次函数上点的坐标特征分别找出两直线与y轴的交点坐标,令其纵坐标相等即可得出结论.
解答 解:当x=0时,y1=b1,y2=b2,
∴直线y1=k1x+b1交y轴于点(0,b1),直线y2=k2x+b2交y轴于点(0,b2),
∴b1=b2.
故选C.
点评 本题考查了一次函数图象上点的坐标特征,解题的关键是根据一次函数图象上点的坐标特征分别找出两直线与y轴的交点坐标.

练习册系列答案
相关题目
20.已知方程4ax-2x+1=-3的解为x=1,那么2a+$\frac{1}{a}$的值为( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -3 | D. | 3 |
19.一元二次方程2x2+5x+3=0根的判别式的值是( )
| A. | 1 | B. | -1 | C. | 13 | D. | 19 |

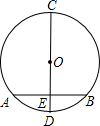 如图,在⊙O中,已知CD是直径,AB是弦,CD⊥AB,垂足为E.
如图,在⊙O中,已知CD是直径,AB是弦,CD⊥AB,垂足为E.