题目内容
如图,抛物线经过点A(1,0),B(5,0),C(0,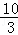 )三点,设点E(x,y)是抛物线上一动点,且在x轴下方,四边
)三点,设点E(x,y)是抛物线上一动点,且在x轴下方,四边 形OEBF是以OB为对角线的平行四边形.
形OEBF是以OB为对角线的平行四边形.
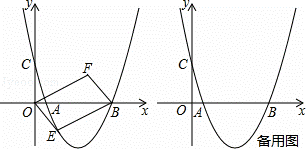
(1)求抛物线的解析式;
(2)当点E(x,y)运动时,试求平行四边形OEBF的面积S与x之间的函数关系式,并求出面积S的最大值?
(3)是否存在这样的点E,使平行四边形OEBF为正方形?若存在,求E点,F点的坐标;若不存在,请说明理由.
解:(1)设所求抛物线的解析式为y=ax2+bx+c,
∵抛物线经过点A(1,0),B(5,0),C(0,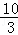 )三点,则由题意可得:
)三点,则由题意可得:
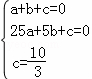 ,解得
,解得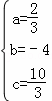 .
.
∴所求抛物线的解析式为:y=x2﹣4x+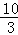 .
.
(2)∵点E(x,y)是抛物线上一动点,且在x轴下方,
∴y<0,
即﹣y>0,﹣y表示点E到OA的距离.
∵OB是平行四边形OEBF的对角线,
∴S=2S△OBE=2××OB•|y|=﹣5y=﹣5(x2﹣4x+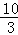 )=﹣
)=﹣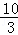 x2+20x﹣
x2+20x﹣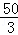 ,
,
∵S=﹣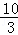 (x﹣3)2+
(x﹣3)2+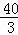
∴S与x之间的函数关系式为:S=﹣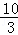 x2+20x﹣
x2+20x﹣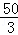 (1<x<5),S的最大值为
(1<x<5),S的最大值为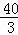 .
.
(3)∵当OB⊥EF,且OB=EF时,平行四边形OEBF是正方形,
∴此时点E坐标只能(,﹣),而坐标为(,﹣)点在抛物线上,
∴存在点E(,﹣),使平行四边形OEBF为正方形,
此时点F坐标为(,).

练习册系列答案
相关题目
如图所示,几何体的主视图是( )

|
| A. |
| B. |
| C. |
| D. |
|
下列运算正确的是( )
|
| A. | a2+a3=a5 | B. | (﹣2a2)3=﹣6a6 | C. | (2a+1)(2a﹣1)=2a2﹣1 | D. | (2a3﹣a2)÷a2=2a﹣1 |
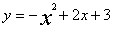 与坐标轴分别交于A、D、B三点,顶点为C。
与坐标轴分别交于A、D、B三点,顶点为C。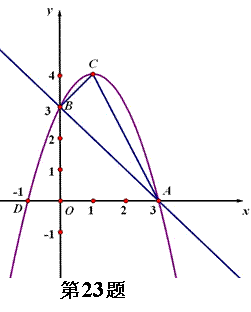 (3)Q是抛物线上一动点,使得以A、B、C、Q为端点的四边形是一个梯形,请直接写出满足条件的Q点的坐标。(不要求写出解题过程)
(3)Q是抛物线上一动点,使得以A、B、C、Q为端点的四边形是一个梯形,请直接写出满足条件的Q点的坐标。(不要求写出解题过程)

 .
.





 的整数解.
的整数解.