题目内容
将一条长为20cm的铁丝剪成两段,并以每一段铁丝的长度为周长各做成一个正方形,求这两个正方形面积之和的最小值.
考点:一元二次方程的应用
专题:几何图形问题
分析:设其中的一段为xcm,则另一段为(20-x)cm,两个正方形的面积之和为y,根据正方形的面积公式建立关系式就可以求出结论.
解答:解:设其中的一段为xcm,则另一段为(20-x)cm,两个正方形的面积之和为y,由题意,得
y=
+
,
y=
(x-10)2+
.
∵a=
>0,
∴抛物线的开口向上,
∴x=10时,y最小=
.
答:这两个正方形面积之和的最小值是
cm2.
y=
| x2 |
| 16 |
| (20-x)2 |
| 16 |
y=
| 1 |
| 8 |
| 25 |
| 4 |
∵a=
| 1 |
| 8 |
∴抛物线的开口向上,
∴x=10时,y最小=
| 25 |
| 4 |
答:这两个正方形面积之和的最小值是
| 25 |
| 4 |
点评:本题考查了正方形的面积公式的运用,二次函数的解析式的运用,二次函数的最值的运用,解答时求出面积之和y与x的关系式是关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
 某制床厂做了一个每晚睡眠时间的统计,结果如图所示.
某制床厂做了一个每晚睡眠时间的统计,结果如图所示.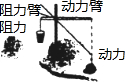 一杠杆装置如图,杆的一端拉起一物体,所受重力为300N.物体对杆的拉力的作用点到支点的杠长为1m.杠与水平线的倾斜角为45°,设在杠的另一端施加的压力为F(N),压力作用点到支点的距离为d(m)(杠杆自身的重量忽略不计).
一杠杆装置如图,杆的一端拉起一物体,所受重力为300N.物体对杆的拉力的作用点到支点的杠长为1m.杠与水平线的倾斜角为45°,设在杠的另一端施加的压力为F(N),压力作用点到支点的距离为d(m)(杠杆自身的重量忽略不计).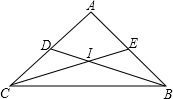 如图,在△ABC中,角平分线BD,CE相交于点I,则∠BIC与∠A有什么关系?如果设∠A为α,求∠BIC(用α表示).利用上述关系,计算:
如图,在△ABC中,角平分线BD,CE相交于点I,则∠BIC与∠A有什么关系?如果设∠A为α,求∠BIC(用α表示).利用上述关系,计算: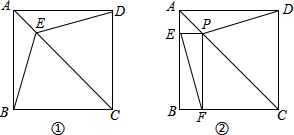 如图①,在正方形ABCD中,点E在AC上.
如图①,在正方形ABCD中,点E在AC上.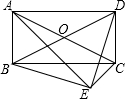 如图,在平行四边形ABCD中,以AC为斜边作Rt△ACE,且∠BED是直角.求证:平行四边形ABCD是矩形.
如图,在平行四边形ABCD中,以AC为斜边作Rt△ACE,且∠BED是直角.求证:平行四边形ABCD是矩形.