题目内容
15.计算:-23+$\frac{1}{3}$×(2005+3)0-(-$\frac{1}{3}$)-2.分析 首先根据负整数指数幂、零指数幂的运算方法方法,求出(2005+3)0、(-$\frac{1}{3}$)-2的值各是多少;然后根据实数混合运算的运算顺序,先计算乘法,再从左向右依次计算即可.
解答 解:-23+$\frac{1}{3}$×(2005+3)0-(-$\frac{1}{3}$)-2
=-8+$\frac{1}{3}×1-9$
=$-8+\frac{1}{3}-9$
=$-8-9+\frac{1}{3}$
=-17$+\frac{1}{3}$
=-$\frac{50}{3}$
点评 (1)此题主要考查了负整数指数幂的运算,要熟练掌握,解答此题的关键是要明确:(1)a-p=$\frac{1}{{a}^{p}}$(a≠0,p为正整数);(2)计算负整数指数幂时,一定要根据负整数指数幂的意义计算;(3)当底数是分数时,只要把分子、分母颠倒,负指数就可变为正指数.
(2)此题还考查了零指数幂的运算,要熟练掌握,解答此题的关键是要明确:(1)a0=1(a≠0);(2)00≠1.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
7.下列计算正确的是( )
| A. | m3-m2=m | B. | -(-3)=3 | C. | (m+n)2=m2+n2 | D. | (3x)2=6x2 |
20.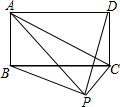 已知矩形ABCD,当点P在图中的位置时,则有结论( )
已知矩形ABCD,当点P在图中的位置时,则有结论( )
 已知矩形ABCD,当点P在图中的位置时,则有结论( )
已知矩形ABCD,当点P在图中的位置时,则有结论( )| A. | S△PBC=S△PAC+S△PCD | B. | S△PBC=S△PAC-S△PCD | ||
| C. | S△PAB+S△PCD=$\frac{1}{2}$S矩形ABCD | D. | S△PAB+S△PCD<$\frac{1}{2}$S矩形ABCD |
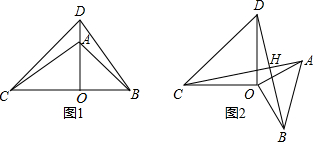 如图,△AOB与△COD都是等腰直角三角形.
如图,△AOB与△COD都是等腰直角三角形.
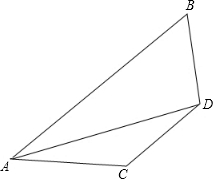 如图所示,已知AD平分∠BAC,∠ACD+∠B=180°,求证:BD=CD.
如图所示,已知AD平分∠BAC,∠ACD+∠B=180°,求证:BD=CD.