题目内容
如图，已知在梯形ABCD中，EF∥AD∥BC，AE=3，EB=5，AD=4，BC=12．那么EF=7
7
．分析：先连接AC，根据EF∥AD∥BC，得出
=
，
=
，然后根据AE=3，EB=5，AD=4，BC=12，分别求出EG、FG的长，即可求出答案．
| AE |
| AB |
| EG |
| BC |
| CF |
| CD |
| GF |
| AD |
解答：解：连接AC与EF相交于点G，
∵EF∥BC，
∴
=
，
∵AE=3，EB=5，
∴AB=AE+BE=3+5=8，
∵BC=12，
∴
=
，
∴EG=
，
∵EF∥AD，
∴
=
，
∵EF∥AD∥BC，
∴
=
=
，
∴
=
，
∵AD=4，
∴
=
，
∴GF=
，
∴EF=EG+GF=
+
=7．
故答案为：7．
∵EF∥BC，
∴
| AE |
| AB |
| EG |
| BC |
∵AE=3，EB=5，
∴AB=AE+BE=3+5=8，
∵BC=12，
∴
| 3 |
| 8 |
| EG |
| 12 |
∴EG=
| 9 |
| 2 |
∵EF∥AD，
∴
| CF |
| CD |
| GF |
| AD |
∵EF∥AD∥BC，
∴
| CF |
| CD |
| BE |
| AB |
| 5 |
| 8 |
∴
| GF |
| AD |
| 5 |
| 8 |
∵AD=4，
∴
| GF |
| 4 |
| 5 |
| 8 |
∴GF=
| 5 |
| 2 |
∴EF=EG+GF=
| 9 |
| 2 |
| 5 |
| 2 |
故答案为：7．
点评：此题考查了相似三角形，用到的知识点是：相似三角形的判定与性质、平行线分线段成比例定理，关键是做出辅助线，构造相似三角形．
练习册系列答案
相关题目
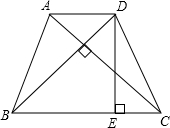如图，已知在梯形ABCD中，AD∥BC，AB=DC，且AC⊥BD，AC=6，则该梯形的高DE等于
9、如图，已知在梯形ABCD中，AD∥BC，AB=DC，对角线AC和BD相交于点O，E是BC边上一个动点（E点不与B、C两点重合），EF∥BD交AC于点F，EG∥AC交BD于点G．
27、如图，已知在梯形ABCD中，AD∥BC，AD+BC=CD，M是AB的中点，DM，CM是否分别是∠ADC和∠DCB的平分线？说明理由．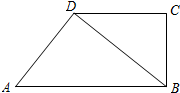
如图，已知在梯形ABCD中，AB∥CD，BC⊥AB，且AD⊥BD，CD=2，
如图，已知在梯形ABCD中，AD∥BC，点E在边BC上，连接DE，AC．