题目内容
13. 901班的全体同学根据自己的兴趣爱好参加了六个学生社团(每个学生必须参加且只参加一个),为了了解学生参加社团的情况,学生会对该班参加各个社团的人数进行了统计,绘制成了如图不完整的扇形统计图,已知参加“读书社”的学生有15人,请解答下列问题:
901班的全体同学根据自己的兴趣爱好参加了六个学生社团(每个学生必须参加且只参加一个),为了了解学生参加社团的情况,学生会对该班参加各个社团的人数进行了统计,绘制成了如图不完整的扇形统计图,已知参加“读书社”的学生有15人,请解答下列问题:(1)该班的学生共有60名;
(2)若该班参加“吉他社”与“街舞社”的人数相同,请你计算,“吉他社”对应扇形的圆心角的度数;
(3)901班学生甲、乙、丙是“爱心社”的优秀社员,现要从这三名学生中随机选两名学生参加“社区义工”活动,请你用画树状图或列表的方法求出恰好选中甲和乙的概率.
分析 (1)利用参加“读书社”的学生数除以所占比例进而求出总人数;
(2)首先求出参加“吉他社”的学生在全班学生中所占比例,进而求出对应扇形的圆心角的度数;
(3)首先画出树状图,进而求出恰好选中甲和乙的概率.
解答 解:(1)∵参加“读书社”的学生有15人,且在扇形统计图中,所占比例为:25%,
∴该班的学生共有:15÷25%=60(人);
故答案为:60;
(2)参加“吉他社”的学生在全班学生中所占比例为:
$\frac{1-25%-20%-20%-15%}{2}$=10%,
所以,“吉他社”对应扇形的圆心角的度数为:360°×10%=36°;
(3)画树状图如下: ,
,
由树状图可知,共有6种可能的情况,其中恰好选中甲和乙的情况有2种,
故P(选中甲和乙)=$\frac{2}{6}$=$\frac{1}{3}$.
点评 此题考查了扇形统计图以及树状图法求概率,弄清题意得出正确信息是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.如图,在数轴上表示1、$\sqrt{3}$的对应点分别为A、B,B关于点A的对称点为点C,则点C所表示的数是( )

| A. | $\sqrt{3}$-2 | B. | 2-$\sqrt{3}$ | C. | $\sqrt{3}$-1 | D. | 1-$\sqrt{3}$ |
 如图,在图中求作⊙P,使⊙P满足以线段MN为弦且圆心P到∠AOB两边的距离相等.(要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔加黑)
如图,在图中求作⊙P,使⊙P满足以线段MN为弦且圆心P到∠AOB两边的距离相等.(要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔加黑) 如图是某儿童乐园为小朋友设计的滑梯平面图.已知BC=4米,AB=6米,中间平台宽度DE=1米,EN、DM、CB为三根垂直于AB的支柱,垂足分别为N、M、B,∠EAB=31°,DF⊥BC于F,∠CDF=45°.求DM和BC的水平距离BM的长度.(结果精确到0.1米,参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
如图是某儿童乐园为小朋友设计的滑梯平面图.已知BC=4米,AB=6米,中间平台宽度DE=1米,EN、DM、CB为三根垂直于AB的支柱,垂足分别为N、M、B,∠EAB=31°,DF⊥BC于F,∠CDF=45°.求DM和BC的水平距离BM的长度.(结果精确到0.1米,参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
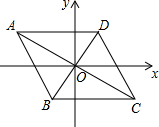 如图,已知点A(-4,2),B(-1,-2),平行四边形ABCD的对角线交于坐标原点O.
如图,已知点A(-4,2),B(-1,-2),平行四边形ABCD的对角线交于坐标原点O. 如图,AB为半圆O在直径,AD、BC分别切⊙O于A、B两点,CD切⊙O于点E,连接OD、OC,下列结论:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2,④OD:OC=DE:EC,⑤OD2=DE•CD,正确的有( )
如图,AB为半圆O在直径,AD、BC分别切⊙O于A、B两点,CD切⊙O于点E,连接OD、OC,下列结论:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2,④OD:OC=DE:EC,⑤OD2=DE•CD,正确的有( ) 等腰△ABC的底角为72°,腰AB的垂直平分线交另一腰AC于点E,垂足为D,连接BE,则∠EBC的度数为36°.
等腰△ABC的底角为72°,腰AB的垂直平分线交另一腰AC于点E,垂足为D,连接BE,则∠EBC的度数为36°.