题目内容
 已知:如图,AM,CM分别平分∠BAD和∠BCD,若∠B=m°,∠D=n°,试说明:∠M=
已知:如图,AM,CM分别平分∠BAD和∠BCD,若∠B=m°,∠D=n°,试说明:∠M=| 1 | 2 |
分析:分别根据∠MOB是△AOB与△OCM的外角,∠MHD是△OCM与△CDH的外角可得出∠MOB=∠B+∠BAM,∠MOB=∠M+∠BCM;∠MHD=∠D+∠DCM,∠MHD=∠M+∠DAM,再由角平分线的性质即可求解.
解答: 解:如图所示,
解:如图所示,
∵∠MOB是△AOB与△OCM的外角.
∴∠MOB=∠B+∠BAM,∠MOB=∠M+∠BCM;
同理,∠MHD是△AHM与△CDH的外角,
∴∠MHD=∠D+∠DCM,∠MHD=∠M+∠DAM,
∴∠B+∠BAM=∠M+∠BCM…①,
∠D+∠DCM=∠M+∠DAM…②,
①+②得∠B+∠BAM+∠D+∠DCM=∠M+∠BCM+∠M+∠DAM.
又∵AM是∠BAD的角平分线,MC是∠BCD的角平分线,
∴∠B+∠D=∠M+∠M,即∠M=
(∠B+∠D).
 解:如图所示,
解:如图所示,∵∠MOB是△AOB与△OCM的外角.
∴∠MOB=∠B+∠BAM,∠MOB=∠M+∠BCM;
同理,∠MHD是△AHM与△CDH的外角,
∴∠MHD=∠D+∠DCM,∠MHD=∠M+∠DAM,
∴∠B+∠BAM=∠M+∠BCM…①,
∠D+∠DCM=∠M+∠DAM…②,
①+②得∠B+∠BAM+∠D+∠DCM=∠M+∠BCM+∠M+∠DAM.
又∵AM是∠BAD的角平分线,MC是∠BCD的角平分线,
∴∠B+∠D=∠M+∠M,即∠M=
| 1 |
| 2 |
点评:本题考查的是三角形外角的性质及角平分线的性质,即三角形的一个外角等于与它不相邻的两个内角的和.

练习册系列答案
相关题目
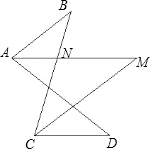 附加题:已知:如图,AM,CM分别平分∠BAD和∠BCD,
附加题:已知:如图,AM,CM分别平分∠BAD和∠BCD, 25、已知:如图,AM是△ABC的中线,∠DAM=∠BAM,CD∥AB.
25、已知:如图,AM是△ABC的中线,∠DAM=∠BAM,CD∥AB. 已知:如图,AM、CM分别平分∠BAD和∠BCD,
已知:如图,AM、CM分别平分∠BAD和∠BCD, 已知:如图,AM是△ABC的中线,∠DAM=∠BAM,CD∥AB.
已知:如图,AM是△ABC的中线,∠DAM=∠BAM,CD∥AB.