题目内容
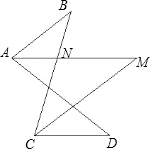 附加题:已知:如图,AM,CM分别平分∠BAD和∠BCD,
附加题:已知:如图,AM,CM分别平分∠BAD和∠BCD,①若∠B=32°,∠D=38°,求∠M的大小;
②若∠B=m°,∠D=n°,试说明∠M=
| 1 | 2 |
分析:利用“三角形的外角等于与它不相邻的两个内角和”作为相等关系列式求解即可.
解答: 解:①∵∠MCD=∠MCB,∠BAM=∠MAD,
解:①∵∠MCD=∠MCB,∠BAM=∠MAD,
∴∠MCD+38°=∠MAD+∠M,∠BAM+32°=∠BCM+∠M,
∴∠MCD-∠MAD+38°=∠M,∠BAM-∠BCM+32°=∠M,
32°+∠BAM+∠MAD=∠BCM+∠MCD+38°,
2∠BAM+32°=2∠MCD+38°,
2∠BAM-2∠MCD=6°,
∠BAM-∠MCD=3°,
∠MAD-∠BCM=3°,
∴∠M=3°+32°=35°;
②如图:∵AM,CM分别平分∠BAD和∠BCD,
∴∠BAM=∠MAD,∠MCB=∠MCD,
∵∠ANC=∠B+∠BAM=∠M+∠MCB,∠AEC=∠MCD+∠D=∠MAD+∠M,
∴∠M=∠B+∠BAM-∠MCB①,
∠M=∠MCD+∠D-∠MAD②,
∴①+②得:2∠M=∠B+∠D,
∴∠M=
(∠B+∠D).
 解:①∵∠MCD=∠MCB,∠BAM=∠MAD,
解:①∵∠MCD=∠MCB,∠BAM=∠MAD,∴∠MCD+38°=∠MAD+∠M,∠BAM+32°=∠BCM+∠M,
∴∠MCD-∠MAD+38°=∠M,∠BAM-∠BCM+32°=∠M,
32°+∠BAM+∠MAD=∠BCM+∠MCD+38°,
2∠BAM+32°=2∠MCD+38°,
2∠BAM-2∠MCD=6°,
∠BAM-∠MCD=3°,
∠MAD-∠BCM=3°,
∴∠M=3°+32°=35°;
②如图:∵AM,CM分别平分∠BAD和∠BCD,
∴∠BAM=∠MAD,∠MCB=∠MCD,
∵∠ANC=∠B+∠BAM=∠M+∠MCB,∠AEC=∠MCD+∠D=∠MAD+∠M,
∴∠M=∠B+∠BAM-∠MCB①,
∠M=∠MCD+∠D-∠MAD②,
∴①+②得:2∠M=∠B+∠D,
∴∠M=
| 1 |
| 2 |
点评:主要考查了三角形的内角和外角之间的关系.(1)三角形的外角等于与它不相邻的两个内角和;(2)三角形的内角和是180度.求角的度数常常要用到“三角形的内角和是180°这一隐含的条件.

练习册系列答案
相关题目
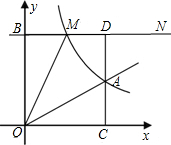 附加题:已知:如图,正比例函数y=ax的图象与反比例函数y=
附加题:已知:如图,正比例函数y=ax的图象与反比例函数y=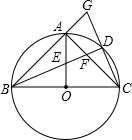 AC分别交于点E、F延长BA、CD交于G.
AC分别交于点E、F延长BA、CD交于G.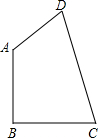 附加题:已知,如图,四边形ABCD中,AB=BC=1,CD=
附加题:已知,如图,四边形ABCD中,AB=BC=1,CD= 20、附加题:已知:如图,a∥b,∠1=70°,则∠3的度数为
20、附加题:已知:如图,a∥b,∠1=70°,则∠3的度数为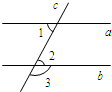 28、(附加题)已知:如图,a∥b,∠1=70°,则∠3的度数为
28、(附加题)已知:如图,a∥b,∠1=70°,则∠3的度数为