题目内容
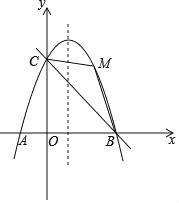
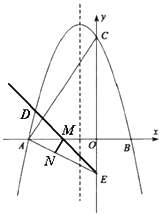
【题目】如图示,在平面直角坐标系中,二次函数![]() (
(![]() )交
)交![]() 轴于
轴于![]() ,
,![]() ,在
,在![]() 轴上有一点
轴上有一点![]() ,连接
,连接![]() .
.
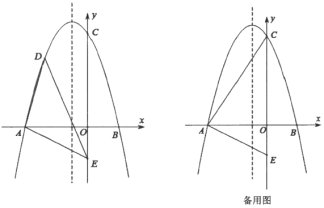
(1)求二次函数的表达式;
(2)点![]() 是第二象限内的点抛物线上一动点
是第二象限内的点抛物线上一动点
①求![]() 面积最大值并写出此时点
面积最大值并写出此时点![]() 的坐标;
的坐标;
②若![]() ,求此时点
,求此时点![]() 坐标;
坐标;
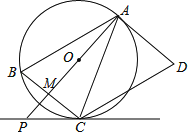
(3)连接![]() ,点
,点![]() 是线段
是线段![]() 上的动点.连接
上的动点.连接![]() ,把线段
,把线段![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() 至
至![]() ,点
,点![]() 是点
是点![]() 的对应点.当动点
的对应点.当动点![]() 从点
从点![]() 运动到点
运动到点![]() ,则动点
,则动点![]() 所经过的路径长等于______(直接写出答案)
所经过的路径长等于______(直接写出答案)
【答案】(1)![]() ;(2)①
;(2)①![]() ,点
,点![]() 坐标为
坐标为![]() ;②
;②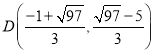 ;(3)
;(3)![]()
【解析】
(1)根据点坐标代入解析式即可得解;
(2)①由A、E两点坐标得出直线AE解析式,设点![]() 坐标为
坐标为![]() ,过点
,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,则
,则![]() 坐标为
坐标为![]() ,然后构建
,然后构建![]() 面积与t的二次函数,即可得出
面积与t的二次函数,即可得出![]() 面积最大值和点D的坐标;
面积最大值和点D的坐标;
②过点![]() 作
作![]() ,在
,在![]() 中,由
中,由![]() ,
,![]() ,
,![]() 得出点M的坐标,进而得出直线ME的解析式,联立直线ME和二次函数,即可得出此时点D的坐标;
得出点M的坐标,进而得出直线ME的解析式,联立直线ME和二次函数,即可得出此时点D的坐标;
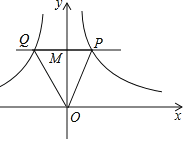
(3)根据题意,当点P在点C时,Q点坐标为(-6,6),当点P移动到点A时,Q′点坐标为(-4,-4),动点![]() 所经过的路径是直线QQ′,求出两点之间的距离即可得解.
所经过的路径是直线QQ′,求出两点之间的距离即可得解.
(1)依题意得:![]() ,解得
,解得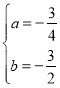
∴![]()
(2)①∵![]() ,
,![]()
∴设直线AE为![]()
将A、E代入,得![]()
∴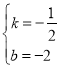
∴直线![]()
设点![]() 坐标为
坐标为![]() ,其中
,其中![]()
过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,则
,则![]() 坐标为
坐标为![]()
∴![]()
∴![]()
即:![]()
由函数知识可知,当![]() 时,
时,![]() ,点
,点![]() 坐标为
坐标为![]()
②设![]() 与
与![]() 相交于点
相交于点![]()
过点![]() 作
作![]() ,垂足为
,垂足为![]()
在![]() 中,
中,![]() ,
,![]() ,
,![]()
设![]() ,则
,则![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴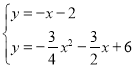
∴![]()
∴![]() (舍去),
(舍去),![]()
当![]() 时,
时,![]()
∴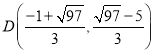
(3)当点P在点C时,Q点坐标为(-6,6),当点P移动到点A时,Q′点坐标为(-4,-4),如图所示:
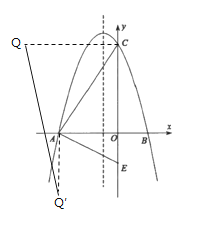
∴动点![]() 所经过的路径是直线QQ′,
所经过的路径是直线QQ′,
∴![]()
故答案为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目