Question

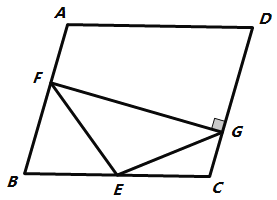
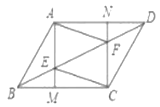
【题目】如图，已知平行四边形，过作于，交于，过作于，交于，连接、．

（1）求证：四边形为平行四边形；

（2）当为菱形，点为的中点时，求的度数．

Answer 1

【答案】（1）见详解 （2）30°

【解析】

（1）根据平行四边形的性质、垂直的定义、平行线的判定定理可以推知AE//CF，然后由全等三角形的判定定理ASA推知△ADE≌△CBF，最后根据全等三角形的对应边相等知AE=CF，所以对边平行且相等的四边形是平行四边形；
（2）根据M是BC的中点，AM⊥BC(已知)，得到△ABC为等边三角形，然后根据三线合一定理即可求解．

证明：（1）∵AM⊥BC，
∴∠AMB=90°，
∵CN⊥AD
∴∠CNA=90°．

∴CN∥AM
∵四边形ABCD是平行四边形，
∴BC∥AD，AD=BC
∴∠ADE=∠CBF，
∵AM∥CN，
又∵∠DAE=∠BCF=90°，
∴△ADE≌△CBF(ASA)，
∴AE=CF，
∴四边形AECF为平行四边形;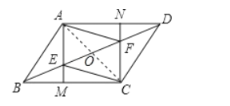

（2）当AECF为菱形时，连结AＣ交BF于点Ｏ，则AＣ与EF互相垂直平分，
又∵OB＝OD

∴AC与BD互相垂直平方，

∴四边形ABCD是菱形，
∴AB=BC，

又∵AM⊥BC，AM=BM，AM=AM

∴△AMB≌△AMC(SAS)

∴AB=AC
即AB=AC=BC，

∴△ABC是等边三角形，
∴∠ABC=60°

∴∠CBD=∠ABC=30°