题目内容
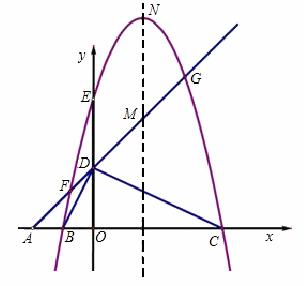
如图,在平面直角坐标系中,已知点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(点P与F、G不重合),作PQ∥y轴与抛物线交于点Q.
(1)若经过B、E、C三点的抛物线的解析式为y=-x2+(2b-1)x+c-5,则b=_____,c=_____(直接填空)
(2)①以P、D、E为顶点的三角形是直角三角形,则点P的坐标为_____(直接填空)
②若抛物线顶点为N,又PE+PN的值最小时,求相应点P的坐标.
(3)连结QN,探究四边形PMNQ的形状:
①能否成为平行四边形
②能否成为等腰梯 形?若能,请直接写出点P的坐标;若不能,请说明理由.
形?若能,请直接写出点P的坐标;若不能,请说明理由.
(1)b=2,c=9
(2)①P(2,4)或(1,3)
②P
(4)①若四边形PMNQ为平行四边形时,点P坐标为
②若四边形PMNQ为等腰梯形时,点P坐标 为

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
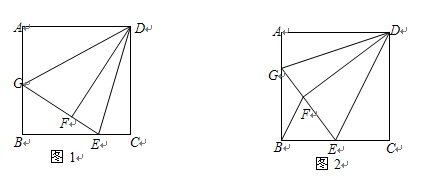
 中,点
中,点 是
是 上的一点,
上的一点, ,点
,点 是
是 的中点.
的中点. ,则
,则 .
. 
 的长.
的长.
 ≈1.732)
≈1.732)
 A.5 B.6 C.7 D.8
A.5 B.6 C.7 D.8

 ,纵坐标不变,所得图形与原图形的关系是
,纵坐标不变,所得图形与原图形的关系是 轴对称 B. 关于
轴对称 B. 关于 轴对称
轴对称 轴向下平移1个单位长度
轴向下平移1个单位长度